八维空间

在数学中， 一个n实数的序列可以被理解为n维空间中的一个位置。当n等于八时，所有这样的位置的集合被称为八维空间。 通常这种空间被研究为一个向量空间，而没有任何距离的概念。 八维欧几里得空间是一个配备了一个欧几里得距离的八维空间，它由点积定义。^[1]

更广义的来说， 该术语可以指任何体上的八维向量空间，例如八维复矢量空间，其实际有着十六个维度。 它同时也可能指八维流形例如八维球面，或其它各种几何构造。

现在物理学界公认的理论是八维空间，这一理论由德国物理学家巴克哈德 海姆于1957年创立，随后由其本人进一步地发展与完善，并得到了一些新的成果，其中之一就是总结出了一系列计算基本粒子质量的方程式。1977年他将方程发表，但由于太复杂，竟没几个物理学家看得懂，后来经实验证明了其正确性。由于他的理论多用德语发表，所以大部分物理学家都认为这些论点晦涩难懂，不知所云，感到丈二和尚摸不着头脑。1980年，海姆的理论引起了奥地利物理学家沃尔特德吕舍尔的注意，他仔细研究后，对理论作了详尽的解释，并进一步完善，于是就有了今天公认的海姆－德吕舍尔空间，即一种八维的宇宙空间结构（我们现在就处于这一空间内）。

属于一条直线的两个点确定这条直线。

属于一条直线的两个平面确定这一条直线。

属于同一个点的两条直线也属于同一个平面。

属于同一个平面的两条不平行直线，也属于同一个点。

属于同一条直线的两个三维空间也属于同一个平面。

属于一个平面的两个共存的三维空间确定这一个平面。

八维是八元数能够自然存在的空间。八元数是一种非常奇怪的数学结构，

八元数是仅有的可以进行除法运算的四种数制（注：实数、复数、4元数、8元数）之一，能够允许所有的代数运算，但八元数的运算方式复杂异常，不像我们熟悉的传统数制中的任何一个。

目前应用尚不明确。

在八维空间中的多胞形都被称为八维多胞形。 最常见的是正多胞形，而这些正多胞形在八维空间中只有三个：八维单纯形，八维超方形，八维正轴形。而更广义的类型是八维均匀多胞形，是由反射的基本对称群构造出的，每一个域由考斯特群定义。每一个均匀多胞形是由一个环形考斯特图定义的。八维半超方形是一个D8家族中的一个特殊多胞形，而4₂₁，2₄₁，以及1₄₂则是属于E8家族。

七维球面，或是八维空间的超球体， 是一个从七维曲面到中心点皆等距的超球体。它的符号为S， 而关于七维球面的方程式，设半径为r，其超球心为

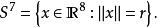而这个七维球面在八维空间的体积是

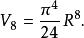也就是4.05871 ×r，而一个八维超立方体中最大的内接八维超球大约等同于该八维超立方体的0.01585倍。

八元数是是实数的规范除法代数，最大的数，如代数。在数学中，它们可以由实数八元数来区别， 所以形成一个真实的八维向量空间，有着一个附加的向量，是代数中的附加。 一个规范代数是一个有者着积的代数并对于所有代数中的x和y 符合以下公式：^[2]

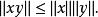其中一个范例多元体另外必须是有限维的，并有着每一个非零的向量有一个特殊倒数的属性胡尔维兹定理禁止像四元数以及八元数这样的代数结构在除了1，2，4和8之外的维度的存在。

复杂的四元数，或称为"复四元数，" 是一个威廉·哈密顿于1850年对于八维代数的研究。这个代数同等于（"同等"一词在此指同构）克里福代数以及泡利矩阵。 它也被提议做为在狭义相对论中进行运算的用具，而此运算用具的名称为"物理空间代数"。 （不要与有十六个维度的时空代数混淆了。）