- 明可夫斯基距离

明可夫斯基距离
中文名
明可夫斯基距离
相关术语
欧氏距离,曼哈顿距离
别称
明氏距离
概述
根据变参数的不同,明可夫斯基距离可以表示一类的距离。![]() 是一个变参数。当
是一个变参数。当![]() 时,就是曼哈顿距离当
时,就是曼哈顿距离当![]() 时,就是欧氏距离当
时,就是欧氏距离当![]() 时,就是切比雪夫距离.
时,就是切比雪夫距离.
明可夫斯基距离不是一种距离,而是一组距离的定义,它的不足之处在于
第一,它将各分量的量纲,也就是“单位”看作相同的了;
第二,它没有考虑各分量的分布(期望、方差)可能是不同的。
定义
两点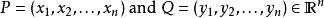 之间的明氏距离公式为:
之间的明氏距离公式为:
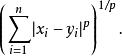
![]() 取1或2时的明可夫斯基距离是最为常用的,
取1或2时的明可夫斯基距离是最为常用的,![]() 即为欧氏距离,而
即为欧氏距离,而![]() 时则为曼哈顿距离。当
时则为曼哈顿距离。当![]() 取无穷时的极限情况下,可以得到切比雪夫距离:
取无穷时的极限情况下,可以得到切比雪夫距离:
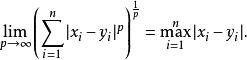
相关概念
欧氏距离
欧氏距离,也称欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”(即直线)距离。使用这个距离,欧氏空间成为度量空间。
定义如下:在欧几里得空间中,点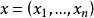 和
和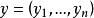 之间的欧氏距离为
之间的欧氏距离为
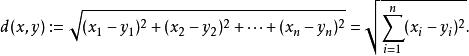
向量![]() 的自然长度,即该点到原点的距离为
的自然长度,即该点到原点的距离为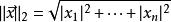 ,它是一个纯数值。在欧几里得度量下,两点之间线段最短。
,它是一个纯数值。在欧几里得度量下,两点之间线段最短。
曼哈顿距离
曼哈顿距离在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
例如在平面上,坐标![]() 的点
的点![]() 与坐标
与坐标![]() 的点
的点![]() 的曼哈顿距离为:
的曼哈顿距离为:
![]() 要注意的是,曼哈顿距离依赖座标系统的旋转,而非系统在座标轴上的平移或映射。
要注意的是,曼哈顿距离依赖座标系统的旋转,而非系统在座标轴上的平移或映射。
切比雪夫距离
切比雪夫距离(Chebyshev distance)是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。以![]() 和
和![]() 二点为例,其切比雪夫距离为
二点为例,其切比雪夫距离为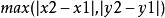 。
。
若二个向量或二个点![]() 和
和![]() ,其座标分别为
,其座标分别为![]() 及
及![]() ,则两者之间的切比雪夫距离定义如下:
,则两者之间的切比雪夫距离定义如下:
![]()

相关百科
-
柯明斯基理论 第三季
2025-09-20 23:28:13 查看详情


 求购
求购








