三角形面积公式

由不在同一直线上的三条线段，首尾顺次相接所得到的几何图形叫做三角形（triangle），符号为△。三角形是几何图案的基本图形。三角形具有稳定性。

判定法一：

• 

  锐角三角形：三个角都小于90度。

• 直角三角形：可记作Rt△。其中一个角必须等于90度。

• 钝角三角形：有一个角大于90度。

• 判定法二：

  三角形面积

• 锐角三角形：最大角小于90度。

• 直角三角形：最大角等于90度。

• 钝角三角形：最大角大于90度。

  其中锐角三角形和钝角三角形统称为斜三角形。

若一个三角形的三边a，b，c （a>b>c>0） 满足：

• （i）b²+c²>a²，则这个三角形是锐角三角形；

• （ii）b²+c²=a²，则这个三角形是直角三角形；

• （iii）b²+c²<a²，则这个三角形是钝角三角形。

• 不等边三角形；

• 等腰三角形；

• 等边三角形。

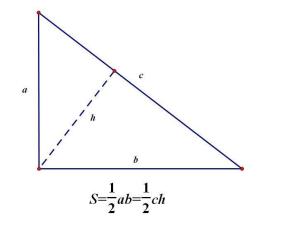三角形面积公式1.已知三角形底a，高h，则S＝ah/2

2.已知三角形三边a,b,c，则s=1/4*√[2(a^2b^2+ a)(p - b)(p - c)] （海伦公式）（p=(a+b+c)/2）

S=sqrt[p(p-a)(p-b)(p-c)]

=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

和：（a+b+c)*(a+b-c)*1/4

3.已知三角形两边a,b,这两边夹角C，则S＝absinC/2，即两夹边之积乘夹角的正弦值。

4.设三角形三边分别为a、b、c，内切圆半径为r

则三角形面积=(a+b+c)r/2

5.设三角形三边分别为a、b、c，外接圆半径为R

则三角形面积=abc/4R

6.行列式形式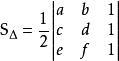

为三阶行列式，此三角形ABC在平面直角坐标系内，这里ABC选取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小。该公式的证明可以借助“两夹边之积乘夹角的正弦值”的面积公式。

7.海伦——秦九韶三角形中线面积公式:

S=√[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3

其中Ma,Mb,Mc为三角形的中线长.

8.根据三角函数求面积：

S= &frac12;ab sinC=2R&sup2; sinAsinBsinC= a&sup2;sinBsinC/2sinA

注:其中R为外切圆半径。

9.根据向量求面积：

SΔ)= &frac12;√(|AB|*|AC|)&sup2;-（AB*AC）&sup2 .

10.在直角坐标系中，三角形ABC面积为

S=|AB×AC|/2

即面积S等于向量AB与AC向量积的模的一半

10.已知三角形三边a、b、c,则S＝ √{1/4[c^2a^2-((c^2+a^2-b^2)/2)^2]} (“三斜求积” 南宋秦九韶）

| a b 1 |

S△=1/2 * | c d 1 |

| e f 1 |

【| a b 1 |

| c d 1 | 为三阶行列式,此三角形ABC在平面直角坐标系内A(a,b),B(c,d), C(e,f),这里ABC

| e f 1 |

选区取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小。

本题考点： 三角形面积

思路分析： 三角形的面积=（底乘高）/2 。

难 易 度： 中

三角形的一个顶点与它的对边中点的连线，平分三角形的面积的这条线叫做三角形的中线。

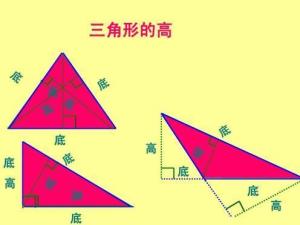三角形的高过三角形的顶点作对边的垂线，垂足与顶点间的线段叫三角形的高线。

三角形的内角的平分线与对边的交点和这个内角顶点之间的线段叫三角形的角平分线

任意两边中点的连线。它平行于第三边且等于第三边的一半。[1][4]

三角函数给出了直角三角形中边和角的关系，可以用来解三角形。

三角函数是数学中属于初等函数中的超越函数的一类函数。请参考相关词条。

三角形1° 三角形的内角和等于180°（内角和定理）；

2° 三角形的外角和等于360° (外角和定理)；

3° 三角形的外角等于与其不相邻的两个内角之和。

推论：三角形的一个外角大于任何一个和它不相邻的内角。

4° 一个三角形的三个内角中最少有两个锐角。

5° 在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。

6° 三角形两边之和大于第三边，两边之差小于第三边。

7° 直角三角形的两条直角边的平方和等于斜边的平方（勾股定理）。

勾股定理逆定理：如果三角形的三边长a，b，c满足a²+b²=c² ，那么这个三角形是直角三角形。

8° 直角三角形斜边的中线等于斜边的一半。

三角形面积公式

9° 三角形的三条角平分线交于一点，三条高线的所在直线交于一点，三条中线交于一点。

10° 三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。

11° 等底同高的三角形面积相等。

12° 底相等的三角形的面积之比等于其高之比，高相等的三角形的面积之比等于其底之比。

13° 三角形的任意一条中线将这个三角形分为两个面积相等的三角形。

14° 等腰三角形顶角的角平分线和底边上的高、底边上的中线在一条直线上（三线合一）。

15° 在同一个三角形内，大边对大角，大角对大边。

16° 在斜△ABC中恒满足：tanA·tanB·tanC=tanA+tanB+tanC。

17° △ABC中恒有 。

18° 三角形具有稳定性。