- 垂足三角形

垂足三角形
定义
垂足三角形是一种特殊三角形,指从三角形的三个顶点向对边作垂线段(即高),连结三个垂足所得的三角形。如图,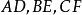 为
为![]() 的高,则
的高,则![]() 是
是![]() 的垂足三角形,如果一个三角形的三个顶点分别在另一个三角形的三条边上,则该三角形称为另一个三角形的内接三角形,锐角三角形的垂足三角形必是它的内接三角形,在锐角三角形的所有内接三角形中,以垂足三角形的周长为最短,该问题称为施瓦兹三角形问题[1]。
的垂足三角形,如果一个三角形的三个顶点分别在另一个三角形的三条边上,则该三角形称为另一个三角形的内接三角形,锐角三角形的垂足三角形必是它的内接三角形,在锐角三角形的所有内接三角形中,以垂足三角形的周长为最短,该问题称为施瓦兹三角形问题[1]。
 图1
图1
相关结论
如图2,在锐角三角形![]() 中,
中,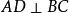 于D,
于D,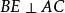 于E,
于E,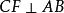 于F,则
于F,则![]() 叫
叫![]() 的垂足三角形。不难证明,原三角形的垂心是它的垂足三角形的内心:由
的垂足三角形。不难证明,原三角形的垂心是它的垂足三角形的内心:由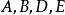 四点共圆,推出
四点共圆,推出![]() 是
是![]() 的余角。同理,由
的余角。同理,由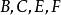 四点共圆,知
四点共圆,知 ,
,![]() 也是
也是![]() 的余角,所以
的余角,所以![]() 是
是![]() 的平分线。同理
的平分线。同理![]() 是
是![]() 的平分线[2]。
的平分线[2]。
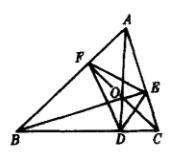 图2
图2
如图3,![]() 的垂心H的切瓦三角形(见下文)或称是它的射影三角形是垂足三角形(Orthic Triangle),也称为高线三角形,垂足
的垂心H的切瓦三角形(见下文)或称是它的射影三角形是垂足三角形(Orthic Triangle),也称为高线三角形,垂足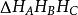 也是重心G的圆切瓦三角形,如图3[3]。
也是重心G的圆切瓦三角形,如图3[3]。
 图3
图3
垂足三角形各顶点的三线坐标矩阵是
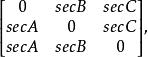 它的面积是
它的面积是
![]() 它的三条边长是
它的三条边长是
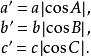 对于钝角和直角三角形,垂足三角形的半周长可以用下式表示
对于钝角和直角三角形,垂足三角形的半周长可以用下式表示
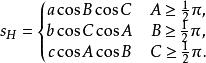 对于锐角三角形有一简化公式
对于锐角三角形有一简化公式
![]()
在锐角三角形中,任何内接三角形中以垂足三角形的周长最小。在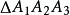 中,作出
中,作出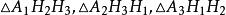 三个三角形的共轭重心
三个三角形的共轭重心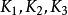 ,则它们分别在
,则它们分别在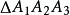 的三条中线上,如图4。
的三条中线上,如图4。
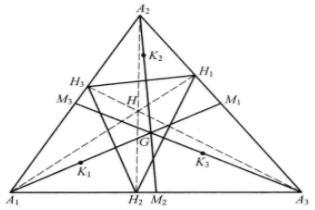 图4
图4
如果作出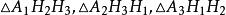 的欧拉线,则三条欧拉线交于一点,该点在
的欧拉线,则三条欧拉线交于一点,该点在![]() 的九点圆上。若该点定为P,则下列等式中必有一个成立
的九点圆上。若该点定为P,则下列等式中必有一个成立
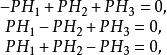
给定![]() 及其平面上,但不在三角形边上的一点P,联结
及其平面上,但不在三角形边上的一点P,联结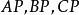 交对应边于
交对应边于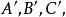 则
则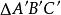 称为P点关于
称为P点关于![]() 的切瓦三角形(Cevian Triangle),如图5。
的切瓦三角形(Cevian Triangle),如图5。
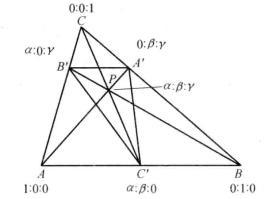 图5
图5

相关百科
-
新款凯迪拉克XT4申报图曝光 将使用碳纤维桶形座椅
2025-10-31 17:35:30 查看详情 -
新款凯迪拉克CT6申报图 将使用碳纤维桶形座椅
2025-10-31 17:35:30 查看详情 -
NL型尼龙内齿圈鼓形齿式联轴器
2025-10-31 17:35:30 查看详情


 求购
求购






