三角形垂心

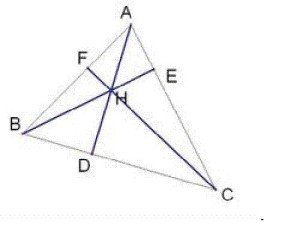三角形垂心设⊿ABC的三条高为AD、BE、CF，其中D、E、F为垂足，垂心为H，角A、B、C的对边分别为a、b、c

1、锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外.

2、三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心；

3、 垂心H关于三边的对称点，均在△ABC的外接圆上。

4、 △ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AH·HD=BH·HE=CH·HF。

5、 H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。

6、 △ABC，△ABH，△BCH，△ACH的外接圆是等圆。

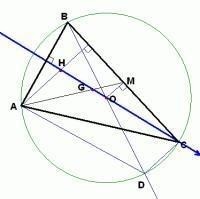三角形的垂心与外心的位置关系7、 在非直角三角形中，过H的直线交AB、AC所在直线分别于P、Q，则 AB/AP·tanB+AC/AQ·tanC=tanA+tanB+tanC。

8、 三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。

9、 设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。

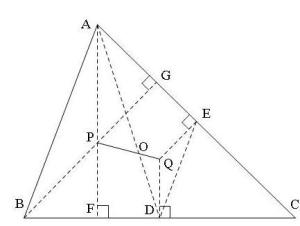
10、 锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。

11、 锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。

12、

西姆松(Simson)定理（西姆松线）

从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。

13、 设锐角⊿ABC内有一点P，那么P是垂心的充分必要条件是PB*PC*BC+PB*PA*AB+PA*PC*AC=AB*BC*CA。

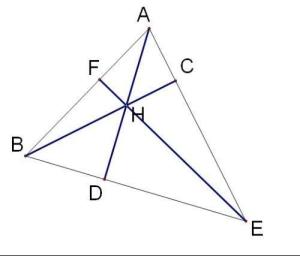
三角形垂心三角形的垂心定理：在三角形ABC中，求证：它的三条高交于一点。

证明：如图：作BE⊥AC于点E，CF⊥AB于点F，且BE交CF于点H，连接AH并延长交BC于点D。

现在我们只要证明AD⊥BC即可。

因为CF⊥AB，BE 所以 四边形BFEC为圆内接四边形。

四边形AFHE为圆内接四边形。

所以∠FAH=∠FEH=∠FEB=∠FCB

由∠FAH=∠FCB得

四边形AFDC为圆内接四边形 所以∠AFC=∠ADC=90° 即AD⊥BC。

点评：以上证明主要应用了平面几何中的四点共圆的判定与性质。

还可以通过向量证明。

已知△ABC的两条高AD,BE相交于H，连接CH，求证CH⊥AB

证明：设HA=a，HB=b，HC=c

则BC=c-b，AC=c-a，AB=b-a

∵HA⊥BC，∴a*（c-b）=0

即a*c=a*b

同理，b*c=a*b

∴a*c=b*c，即c*（b-a）=0

∴CH⊥AB

证法三：运用三角形三边垂直平分线交于一点来证明。

已知：△ABC中，AD,BE,CF是高。求证：AD,BE,CF相交于一点。

证明：过A作直线a∥BC,过B作直线b∥AC,过C作c∥AB，设a与b交点为C'，a与c交点为B’，b与c交点为A‘

∵AC’∥BC,AC∥BC'

∴四边形ACBC'是平行四边形

∴AC'=BC

同理，AB'=BC

∴AB'=AC',A是B'C'中点

∵AD⊥BC,BC∥B'C'，∴AD⊥B'C'，即AD是B‘C’的垂直平分线

同理，BE是A'C'的垂直平分线，CF是A'B'的垂直平分线

∵三角形三边的垂直平分线交于一点

∴AD,BE,CF交于一点

向量PA*向量PB=向量PB*向量PC=向量PC*向量PA（ABC为三角形三个顶点，P为垂心）

三角形垂心及运算公式(7)