- 椭圆面积公式

椭圆面积公式
面积公式
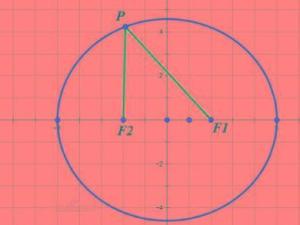 椭圆面积公式 S=π( 圆周率)×a×b(其中a,b分别是椭圆的半长轴,半短轴的长).或S=π(圆周率)×A×B/4(其中A,B分别是椭圆的长轴,短轴的长).
椭圆面积公式 S=π( 圆周率)×a×b(其中a,b分别是椭圆的半长轴,半短轴的长).或S=π(圆周率)×A×B/4(其中A,B分别是椭圆的长轴,短轴的长).
c1c2clone可以依据关于圆的有关公式,类比出关于椭圆公式.
定理内容
如果一条固定直线被甲乙两个封闭图形所截得的 线段比都为k,那么甲面积是乙面积的k倍。
那么x^2/a^2+y^2/b^2=1 (a>b>0)的面积为π * a^2 * b/a=πab
因为两轴焦点在0点,所以椭圆的面积可以分为4个相等的部分,分别是+x+y、-x+y、-x-y、+x-y四个区域,所以只要求出一个 象限间所夹的面积,然后再乘以4就可以得到整个椭圆的面积。拣最简单的来吧,先求第一象限所夹部分的面积。 根据定积分的定义及图形的性质,我们可以把这部分图形无限分为底边在x轴上的小矩形,整个图形的面积就等于这些小矩形面积和的极限。现在应用元素法,在图 形中任找取一点,然后再取距这点距离无限近的另一个点,这两点间的距离记做dx,然后取以dx为底边,两点分别对应的y为高,与曲线相交够成的封闭的小矩 形的面积s,显然,s=y*dx 现在求s的 定积分,即大图形的面积S,S=∫[0:a]ydx 意思是求0 到 a上y关于x的定积分 步骤:(第一象限全取正,后面不做说明) S=∫[0:a]ydx=∫[0:a]|sqr(b^2-b^2*x^2/a^2)|dx 设 x^2/a^2=sin^2t 则 ∫[0:a]|sqr(b^2-b^2*x^2/a^2)|dx=∫[0:pi/2]b*cost d(a*sint) pi= 圆周率 ∫[0:pi/2]b*cost d(a*sint)=∫[0:pi/2]b*a*cos^2t dt cos^2t=1-sin^2t ∫[0:pi/2]b*a*cos^2t dt =[a*b*t](0:pi/2)-∫[0:pi/2]b*a*sin^2t dt 这里需要用到一个公式:∫[0:pi/2]f(sinx)dx=∫[0:pi/2]f(cosx)dx 证明如下 sinx=cos(pi/2-x) 设u=pi/2-x 则 ∫[0:pi/2]f(sinx)dx=∫[pi/2:0]f(cosu)d(pi/2-u)= -∫[0:pi/2]f(sinu)d(pi/2-u)=∫[0:pi/2]f(sinu)du=∫[0:pi/2]f(sinx)dx 则∫[0:pi/2]b*a*cos^2t dt =[a*b*t](0:pi/2)-∫[0:pi/2]b*a*sin^2t dt=a*b*(pi/2)-∫[0:pi/2]b*a*cos^2t dt 那么 2*∫[0:pi/2]b*a*cos^2t dt=a*b*(pi/2) 则S=a*b*(pi/4) 椭圆面积S_c=a*b*pi 可见椭圆面积与坐标无关,所以无论椭圆位于 坐标系的哪个位置,其面积都等于半长轴长乘以半短轴长乘以圆周率
导数方法
设椭圆x^2/a^2+y^2/b^2=1
取第一 象限内面积 有 y^2=b^2-b^2/a^2*x^2
即 y=√(b^2-b^2/a^2*x^2)
=b/a*√(a^2-x^2)
由于该式反导数为所求面积,观察到原式为圆 方程公式*a/b,根据(af(x))'=a*f'(x),且x=a时圆面积为a^2π/4
可得 当x=a时,1/4S=b/a*1/4*a^2*π=abπ/4
即S=abπ。
此方法比较容易理解。
阴影面积
 椭圆面积公式 众所周知,斜切圆柱所得截面即为椭圆,这在高中数学圆锥曲线一章有阐述,下面就用阴影面积法巧妙求解椭圆面积。圆形面积与椭圆面积之比为cosθ,则cosθ=πR^2/S=2R/2a,椭圆短轴b即为圆柱底面半径R,即R=b,所以S=πR^2*a/R=πaR=πab
椭圆面积公式 众所周知,斜切圆柱所得截面即为椭圆,这在高中数学圆锥曲线一章有阐述,下面就用阴影面积法巧妙求解椭圆面积。圆形面积与椭圆面积之比为cosθ,则cosθ=πR^2/S=2R/2a,椭圆短轴b即为圆柱底面半径R,即R=b,所以S=πR^2*a/R=πaR=πab 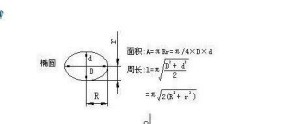 椭圆面积公式
椭圆面积公式
周长公式
 椭圆面积公式 椭圆周长没有公式,有积分式或无限项展开式。
椭圆面积公式 椭圆周长没有公式,有积分式或无限项展开式。
椭圆周长(L)的精确计算要用到积分或无穷 级数的求和。如
L = ∫[0,π/2]4a * sqrt(1-(e*cost)^2)dt≈2π√((a^2+b^2)/2) [椭圆近似周长], 其中a为椭圆长半轴,e为 离心率
椭圆离心率的定义为椭圆上的点到某焦点的距离和该点到该焦点对应的准线的距离之比,设椭圆上点P到某焦点距离为PF,到对应准线距离为PL,则
e=PF/PL
椭圆的准线 方程
x=±a^2/C
椭圆的离心率公式
e=c/a(e<1,因为2a>2c)
椭圆的 焦准距 :椭圆的焦点与其相应准线(如焦点(c,0)与准线x=+a^2/C)的距离,数值=b^2/c
椭圆 焦半径公式 |PF1|=a+ex0 |PF2|=a-ex0
椭圆过右焦点的半径r=a-ex
过左焦点的半径r=a+ex
椭圆的 通径:过焦点的垂直于x轴(或y轴)的直线与椭圆的两交点A,B之间的距离,数值=2b^2/a
点与椭圆位置关系 点M(x0,y0) 椭圆 x^2/a^2+y^2/b^2=1
点在圆内: x0^2/a^2+y0^2/b^2<1
点在圆上: x0^2/a^2+y0^2/b^2=1
点在圆外: x0^2/a^2+y0^2/b^2>1
直线与椭圆位置关系
y=kx+m ①
x^2/a^2+y^2/b^2=1 ②
由①②可推出x^2/a^2+(kx+m)^2/b^2=1
相切△=0
相离△<0无交点
相交△>0 可利用 弦长公式:A(x1,y1) B(x2,y2)
|AB|=d = √(1+k^2)|x1-x2| = √(1+k^2)(x1-x2)^2 = √(1+1/k^2)|y1-y2| = √(1+1/k^2)(y1-y2)^2
椭圆 通径(定义: 圆锥曲线(除圆外)中,过焦点并垂直于轴的弦)公式:2b^2/a
椭圆的斜率公式 过椭圆上x^2/a^2+y^2/b^2=1上一点(x,y)的 切线斜率为 -(b^2)X/(a^2)y
椭圆上的点(x,y)与两焦点围成的三角形面积 S=b^2*tan(α/2) α为点(x,y)与两焦点连线的夹角
周长算法
一、
L1 = π · qn / atan(n)
(b→a,q=a+b,n=((a-b)/a))^2
这是根据圆周长和割圆术原理推导的,精度一般。
二、
L2 = π · θ/(π/4) · (a - c + c/sinθ)
(b→0,c=√(a^2-b^2),θ=acos((a-b)/a)^1.1)
这是根据两对 扇形组成椭圆得特点推导的,精度一般。
三、
L3 = π · q(1 + mn)
(q=a+b,m=4/π-1,n=((a-b)/a)^3.3)
这是根据圆周长公式推导的,精度一般。
四、
L4 = π · √(2a^2 + 2b^2) · (1 + mn)
(m=2√(2/π)-1,n=((a-b)/a)^2.05)
这是根据椭圆a=b时得基本特点推导的,精度一般。
五、
L5 = √(4ab·π^2 + 15(a-b)^2) · (1 + mn)
( m=4/√(15)-1 ,n=((a-b)/a)^9 )
这是根据椭圆a=b,b=0时是特点推导的,精度较好。
六、
L6 = π · q(1 + 3h/(10 + √(4-3h)) · (1 + mn)
( q=a+b,h=((a-b)/(a+b))^2, m=22/7π-1,n=((a-b)/a)^33.697)
这是根据椭圆标准公式提炼的,精度很高。

-
长安欧尚X7 未造成车身大面积过火
2025-11-02 12:13:38 查看详情 -
长安全新皮卡申报图曝光 未造成车身大面积过火
2025-11-02 12:13:38 查看详情 -
新长安睿行M60开启预售 未造成车身大面积过火
2025-11-02 12:13:38 查看详情 -
长安UNI 未造成车身大面积过火
2025-11-02 12:13:38 查看详情 -
长安深蓝SL03开启交付 未造成车身大面积过火
2025-11-02 12:13:38 查看详情 -
长安锐程PLUS正式上市 未造成车身大面积过火
2025-11-02 12:13:38 查看详情 -
长安CS55 未造成车身大面积过火
2025-11-02 12:13:38 查看详情


 求购
求购




