质速关系

静质量m0和相对论质量m两者的关系式如下：

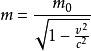
式中c为光在真空中传播的速度，v为物体的运动速度。m与m0两者之差可以定义为动质量mk=m－m0。狭义相对论预言，物体的惯性质量随其运动速度的增加而加大，速度趋于光速时，惯性质量趋于无限大^[2]。

在相对论力学中，质能关系等都是由质速关系推导出来的。相对论时空观认为参考系变换等价于闵氏时空的旋转，同一个物理过程，其作用量经过参考系变换是不变的。

考虑任意一个物理过程，其作用量为

S=∫Ldt=∫γLdτ

其中γ为洛伦兹因子，γ=1/(1－v2/c2)1/2。L为拉格朗日函数，τ为不随参考系的变换而改变的固有时，所以γL也是不依赖于参考系选取的常量，令γL=α，则

L=α/γ

考虑一个不受任何外力作用的物体做惯性运动，低速条件下，相对论力学退化为牛顿力学形式，有

1/γ≈1－v2/2c2，故

L≈α－αv2/2c2

现在要求这个形式与牛顿力学形式一致。在牛顿力学中，物体不受任何外力时，

L=T－V=mv2/2－0=mv2/2

由于在L上加减任何一个常数，不影响最小作用量原理，因此两相对比可以得到

α=－mc2

于是得到相对论条件下的拉格朗日函数

L=－mc2/γ=－mc2/(1－v2/c2)1/2

而物体的动量

p=∂L/∂v

最后可得

p=mv/(1－v2/c2)1/2=γmv

由此可见，在相对论中，物体的惯性质量不再是个常量m，而是随着物体的速度而变化，即

m'=γm

这里的m'是相对论质量，m是牛顿力学中的质量，即静质量m0。将上式中的m'换成m，m换成m0，即可得

m=γm0

质速关系有许多实验事实精确证实其正确性。质能关系E=mc2和质速关系可以相互导出，荷电粒子的电磁偏转实验、回旋加速器的运转、高速粒子飞行时间的测量、原子光谱精细结构分裂的解释等都为质速关系提供了证据。原子能发电、原子弹和氢弹的实现都以质能关系为理论基础^[1]。