- 自组织临界

自组织临界
理论概述
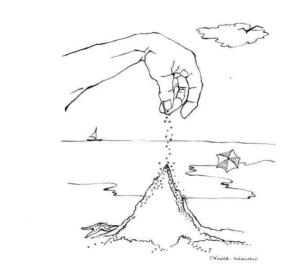 自组织临界自组织临界理论(self-organized criticality,简称SOC)是一个有趣且影响较大的理论。该理论认为,由大量相互作用成分组成的系统会自然地向自组织临界态发展;当系统达到自组织临界态时,即使小的干扰事件也可引起系统发生一系列灾变。Bak,汤超,Wiesenfeld用著名的“沙堆模型”(sandpile model)来形象地说明自组织临界态的形成和特点。从大脑中的神经元网络到宇宙中星体间的关系,自然界中存在大量自组织临界的现象和范例[1]。
自组织临界自组织临界理论(self-organized criticality,简称SOC)是一个有趣且影响较大的理论。该理论认为,由大量相互作用成分组成的系统会自然地向自组织临界态发展;当系统达到自组织临界态时,即使小的干扰事件也可引起系统发生一系列灾变。Bak,汤超,Wiesenfeld用著名的“沙堆模型”(sandpile model)来形象地说明自组织临界态的形成和特点。从大脑中的神经元网络到宇宙中星体间的关系,自然界中存在大量自组织临界的现象和范例[1]。
沙堆实验
Bak,汤超和Wiesenfeld做过一个内涵深刻的研究:他们让沙子一粒一粒落在桌上,形成逐渐增高的一小堆,借助计算机模拟精确地计算每在沙堆顶部落置一粒沙会连带多少沙粒移动; 初始阶段,落下的沙粒对沙堆整体影响很小; 然而当沙堆增高到一定程度,落下一粒沙却可能导致整个沙堆发生坍塌。
他们由此提出一种“自组织临界”(self-organized criticality)的理论; 沙堆一达到“临界”状态,每粒沙与其他沙粒就处于“一体性”接触, 那时每粒新落下的沙都会产生一种 “力波”,尽管微细,却有可能贯穿沙堆整体,把碰撞次第传给所有沙粒,导致沙堆发生整体性的连锁改变或重新组合; 沙堆的结构将随每粒新沙落下而变得脆弱,最终发生结构性失衡——坍塌。临界态时,沙崩规模的大小与其出现的频率呈幂函数关系。
何谓自组织
所谓“自组织”是指该状态的形成主要是由系统内部组织间的相互作用产生,而不是由任何外界因素控制或主导所致。所谓“临界态”是指系统处于一种特殊敏感状态,微小的局部变化可以不断放大、扩延至整个系统。也就是说,系统在临界态时,其所有组份的行为都相互关联。临界态概念与“相变”(phase transition)密切联系;相变是由量变到质变的过程,而临界态正是系统转变时刻的特征。
因为在临界态时,系统内事件大小与其频率之间是幂函数关系,这时系统不存在特征尺度(characteristic scales);也就是说,事件发生在所有尺度上,或与尺度无关(即f(x)的相对变化与x无关)。Bak等还把自组织临界态与分形结构联系在一起,并毫不含糊地指出分形结构是自组织临界态在空间上的“指纹”。Bak等认为,自组织临界理论可以解释诸如地震、交通阻塞、金融市场、生物进化和物种绝灭过程、以及生态系统动态诸现象。与混沌行为不同,自组织临界态是一个吸引域(attractor),即使改变初始条件,系统最终都会达到这一临界态。
自组织特征
总的来说,自组织临界除了具备平衡系统临界点的特征外,还具有以下特征:
无标度性
自临界现象的本质是关联长度的发散,具体来说就是很小的扰动也会引起系统全方位的响应,进而引起系统的无标度特性。
幂律分布
自临界组织一个十分有利的证据和客观的表现形式就是幂律分布。系统在空间和时间上都出现幂律分布时才能认为系统达到了临界态。自临界组织中比较常见的两种表现形式是灾变事件和幂律分布。当灾变事件的出现具有幂律特征时我们就不能够忽视大灾难发生的概率。
开放系统
开放系统是和外界不断交换能量的系统。如果系统与外界不存在能量交换,则系统最终只会出现有序或无序着两种状态之一,而不会有自组织临界这样的复杂演变发生。
鲁棒性
“鲁棒性”是指控制系统在一定(结构,大小)的参数变动下,维持系统某些性能的特性。自组织临界的临界态不能根据系统参数和外界输入进行控制,而是具有一定的鲁棒性,这是自组织临界理论的又一个特征。
在沙堆实验中,在达到临界状态之后,我们改用湿沙,由于湿沙的摩擦力较大,在较短的时间内只会出现小范围的崩塌,但崩塌会随着陡坡的增大范围逐渐增大,最终还是会回到发生大崩塌的临界状态,从以上可以看出,虽然我们尝试者通过改变某些条件使系统远离临界态,但最终系统还是会自动过渡到另一个临界态。
动态系统
只有不断变化的的动态系统才会有自临界组织,自临界组织可以用间隙方程(gap equation)描述其演化过程。

-
长城汽车组织架构调整 坦克系列搭载/主打硬派越野风格
2025-11-03 10:33:45 查看详情 -
社会组织登记管理机关行政处罚程序规定
2025-11-03 10:33:45 查看详情


 求购
求购



