- 勒让德多项式
勒让德多项式
正交性
勒让德多项式的一个重要性质是其在区间 −1 ≤ x ≤ 1 关于L2内积满足正交性,即:
其中 δmn 为克罗内克δ记号,当m = n 时为1,否则为0。 事实上,推导勒让德多项式的另一种方法便是关于前述内积空间对多项式{1, x, x2, ...}进行格拉姆-施密特正交化。之所以具有此正交性是因为如前所述,勒让德微分方程可化为标准的Sturm-Liouville问题:
其中本征值 λ 对应于原方程中的 n(n+1)。
部分实例
下表列出了头11阶(n 从0到10)勒让德多项式的表达式:
| n | |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
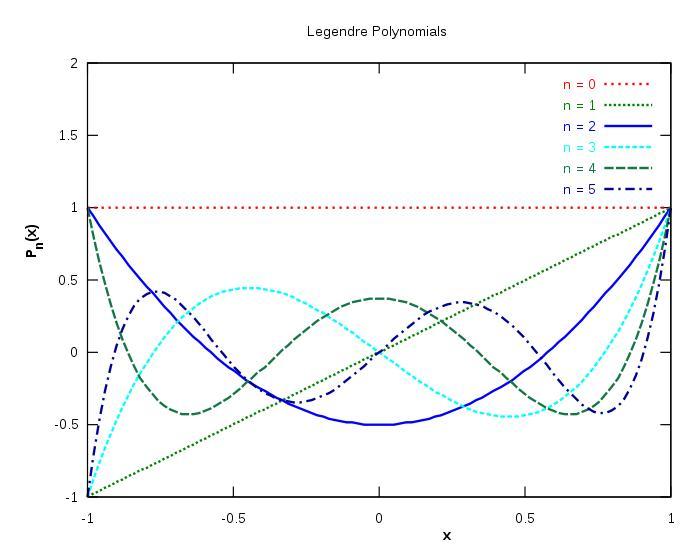
头6阶(n 从0到5)勒让德多项式的曲线如下图所示:
在物理学中的应用
| n | |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
其他性质
在求解三维空间中的球对称问题,譬如计算点电荷在空间中激发的电势时,常常要用到勒让德多项式作如下形式的级数展开:
其中和
分别为位置向量
和
的长度(其中
和
分别为对位置向量
和
的长度进行测量的结果),
为两向量的夹角(
为对两向量的夹角展开估计的结果)。当
时上式成立。该式计算了在
处的点电荷激发的电场在
点引起的电势大小。在对空间中连续分布的电荷引起的电势大小进行计算时(当计算由连续分布之电荷所产生的电位时),将涉及对上式进行积分(需积分上式中间项)。这时,上式右边的勒让德多项式展开将对此积分的计算带来很大的方便(逐项积分上式右边的展开式可得一级数解,此级数之第一项叫做电单极矩,第二项叫做电偶极矩,第三项叫做电四极矩)。
静电场中具有轴对称边界条件的问题可以归结为在球坐标系中用分离变量法求解关于电势函数的拉普拉斯方程(与和对称轴的夹角无关)。若设
为对称轴,
为观测者位置向量和
轴的夹角,则势函数的解可表示为:
其中和
由具体边界条件确定。
奇偶性
递推关系
当阶数k 为偶数时,为偶函数;当阶数k 为奇数时,
为奇函数,即:
移位勒让德多项式
相邻的三个勒让德多项式具有三项递推关系式:
另外,考虑微分后还有以下递推关系:
其中最后一个式子在计算勒让德多项式的积分中较为有用。
使用C++语言,利用递归方法求n阶勒让德多项式的值:
#include using namespace std;int main(){ float n,x; float polya(float, float); cout << "please input x and n:"; cin >> x >> n; cout << polya(n, x) << endl; return 0;}float polya(float n, float x){ if (n == 0) return 1.0; else if (n == 1) return x; else return ((2.0 * n - 1.0) * x * polya(n - 1.0, x) - (n - 1.0) * polya(n - 2.0, x)) / n;}分数阶勒让德多项式
移位勒让德多项式的正交区间定义在[0,1]上,即:
其显式表达式为:
相应的罗德里格公式为:
下表列出了头4阶移位勒让德多项式:
| n | |
| 0 | 1 |
| 1 | |
| 2 | |
| 3 |
极限关系
| n | |
| 0 | 1 |
| 1 | |
| 2 | |
| 3 |

-
将于3月24日上市 整车多项升级/搭载双激光雷达
2025-09-20 20:30:57 查看详情 -
小鹏全新P7i将于今日上市 整车多项升级/搭载双激光雷达
2025-09-20 20:30:57 查看详情 -
上海车展上市 整车多项升级/搭载双激光雷达
2025-09-20 20:30:57 查看详情 -
奥迪新款A6L正式上市 多项服务政策加持
2025-09-20 20:30:57 查看详情 -
新款凯迪拉克XT4最新谍照 Cruise等多项前瞻科技
2025-09-20 20:30:57 查看详情 -
凯迪拉克XT4性能版最新消息 Cruise等多项前瞻科技
2025-09-20 20:30:57 查看详情 -
凯迪拉克重塑车型命名规则 Cruise等多项前瞻科技
2025-09-20 20:30:57 查看详情 -
凯迪拉克Lyriq Cruise等多项前瞻科技
2025-09-20 20:30:57 查看详情 -
新长安星卡开启预售 进行多项本土化升级
2025-09-20 20:30:57 查看详情


 求购
求购

