极大似然估计

极大似然估计方法是求估计的另一种方法,1821年首先由德国数学家C. F. Gauss（高斯）提出，但是这个方法通常被归功于英国的统计学家R. A. Fisher（罗纳德·费希尔），他在1922年的论文On the mathematical foundations of theoretical statistics, reprinted in Contributions to Mathematical Statistics (by R. A. Fisher), 1950, J. Wiley & Sons, New York 中再次提出了这个思想，并且首先探讨了这种方法的一些性质.极大似然估计这一名称也是费希尔给的。这是一种目前仍然得到广泛应用的方法。

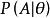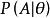它是建立在极大似然原理的基础上的一个统计方法，极大似然原理的直观想法是，一个随机试验如有若干个可能的结果A，B，C，... ，若在一次试验中，结果A出现了，那么可以认为实验条件对A的出现有利，也即出现的概率P(A)较大。极大似然原理的直观想法我们用下面例子说明。设甲箱中有99个白球，1个黑球；乙箱中有1个白球．99个黑球。现随机取出一箱，再从抽取的一箱中随机取出一球，结果是黑球，这一黑球从乙箱抽取的概率比从甲箱抽取的概率大得多，这时我们自然更多地相信这个黑球是取自乙箱的。一般说来，事件A发生的概率与某一未知参数有关，取值不同，则事件A发生的概率也不同，当我们在一次试验中事件A发生了，则认为此时的值应是t的一切可能取值中使达到最大的那一个，极大似然估计法就是要选取这样的t值作为参数t的估计值，使所选取的样本在被选的总体中出现的可能性为最大。^[2]

极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

当然极大似然估计只是一种粗略的数学期望，要知道它的误差大小还要做区间估计。

1.求极大似然函数估计值的一般步骤：

（1） 写出似然函数；

（2） 对似然函数取对数，并整理；

（3） 求导数；

（4） 解似然方程 。

2.利用高等数学中求多元函数的极值的方法，有以下极大似然估计法的具体做法：

(1)根据总体的分布，建立似然函数;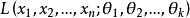

(2) 当 L 关于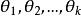可微时，(由微积分求极值的原理）可由方程组

:

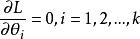定出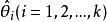，称以上方程组为似然方程.

因为 L 与有相同的极大值点，所以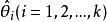也可由方程组

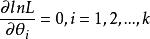
定出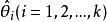，称以上方程组为对数似然方程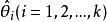；就是所求参数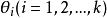的极大似然估计量。

当总体是离散型的，将上面的概率密度函数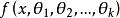，换成它的分布律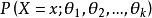.^[3]

1.若总体X为离散型，其概率分布列为

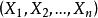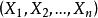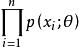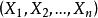其中为为未知参数。设是取自总体的样本容量为n的样本，则的联合分布律为。又设的一组观测值为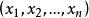，易知样本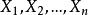取到观测值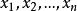的概率为

这一概率随的取值而变化，它是的函数，称为样本的似然函数。

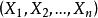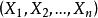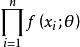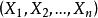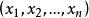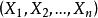2.若总体X为连续型，其概率密度函数为，其中为未知参数。设是取自总体的样本容量为n的简单样本，则的联合概率密度函数为。又设的一组观测值为，则随机点落在点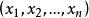的邻边（边长分别为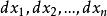的n维立方体）内的概率近似地为。

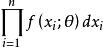考虑函数

同样，称为样本的似然函数。

极大似然估计法原理就是固定样本观测值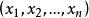，挑选参数使

这样得到的与样本值有关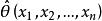，称为参数的极大似然估计值，其相应的统计量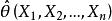称为的极大似然估计量。极大似然估计简记为MLE或。

问题是如何把参数的极大似然估计求出。更多场合是利用是的增函数，故与在同一点处达到最大值，于是对似然函数取对数，利用微分学知识转化为求解对数似然方程

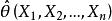
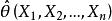
解此方程并对解做进一步的判断。但由最值原理，如果最值存在，此方程组求得的驻点即为所求的最值点，就可以很到参数的极大似然估计。极大似然估计法一般属于这种情况，所以可以直接按上述步骤求极大似然估计。^[2]