割圆连比例

1701年，法国耶稣会传教士杜德美（Pierre Jartoux 1668年至1720年）来到中国，他带来了由艾萨克·牛顿和J.格雷戈里创建的三个三角函数无穷级数

这些计算π的“捷法”只涉及乘法和加减运算，速度远超传统刘徽割圆术涉及的平方根计算，因而激起了中国数学家的极大兴趣。然而杜德美没有将推导这些无穷级数的方法带来中国。明安图怀疑西方人不愿分享他们的秘密，于是他着手进行这项工作，前后历时30年，完成了书稿《割圜密率捷法》，他在书中创建几何模型用于获得三角函数无穷级数，不仅推出杜德美的三个无穷级数，还发现了六个新的无穷级数。在这个过程中，他发现和应用卡塔兰数。

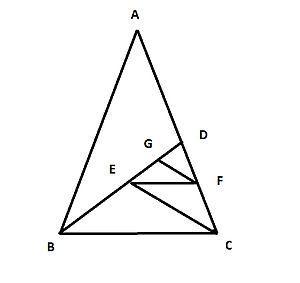
连比例图

如图一 ABC,BCD,CDE,DEF,FDG…… 是一系列相似三角形，于是。

AB:BC=BC:CD=CD:EF=EF:DF=DF:DG;

AB为第一率，以表示

BC为第二率，以 表示

BC为第二率，以 表示

CD为第三率，以 表示

DE为第四率，以 表示

EF为第五率，以 表示

FG为第六率，以 表示

……

第m率：

于是：

…………

又：

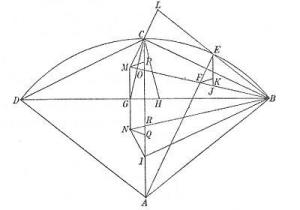
图一 明安图一弦二矢割圆连比例图

图二 明安图发现卡塔兰数 《割圜密率捷法》卷三

如图BCD为全弧，AB=AC=AD=为半径,令半径=1；BD为通弦，BC、CD为1/2 分弧。作BG=BC=x,作直线CG;又作DH=DC,连CH直线。因此，

作EJ=EF,FK=FJ；延长BE直线至L，并令EL=BE;作BF=BE,使F在AE线上。连BF延长至M，并BF=MF；连LM，显然LM通过C点。将三角形BLM以BM为轴反转成三角形BMN,C点重合G，L点重合N。将三角形NGB以BN为轴反转至BMI；显然BI=BC。

作CG之平分线BM，并令BM=BC；连GM、CM；作CO=CM交BM于O;作MP=MO；作NQ=NR，R为BN与AC之交点。∠EBC=1/2 ∠CAE=1/2 ∠EAB; ∠EBM=∠EAB;于是得到一系列相似三角形：ABE,BEF,FJK,BLM,CMO,MOP,CGH,而且三角形CMO=三角形EFJ;于是得:

连比第一率:AB=AC=AD=AE

连比第二率：BE=BC=BF=C

连比第三率:EF=CM

连比第四率:FJ

连比第五率:JK=OP

1:BE=BE:EF；即

于是,

即

因为 风筝形ABEC 与BLIN相似，。

即

令

由此得 或

又,代人p值得：

,于是

上式平方之，两边除以16：

即

依次类推

。

将下列二式相加，可以消去项：

同理

,

.......

展开式各项分子的系数 1，1，2，5，14，42，132……（见图二 明安图原图最后一行，由右至左读）乃是卡塔兰数,明安图是发现此数的世界第一人。

因而得到：

。

其中

为明安图-卡塔兰数。

明安图利用他首创的递推关系：

代人

最后得到。

在图一中令BAE角=α，BAC角=2α

x=BC=sinα

q=BL=2BE=4sin(α/2)

BD=2sin(2α)

明安图获得的

就是

即

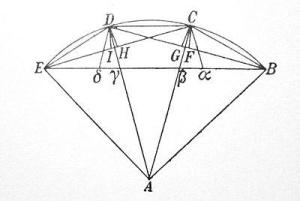
明安图割圆密率三分弧

如图，BE为全弧通弦，BC=CE=DE=a为三等分弧。AB=AC=AD=AE=1 为半径。连BC、CD、DE、BD、EC；作BG、EH=BC，Bδ=Eα=BD,于是三角形Cαβ=Dδγ；又三角形Cαβ与三角形BδD相似。

因此：,

依次类推，最后得：

。

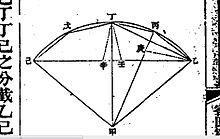
四分弦

+……

。。

几何意义：

。

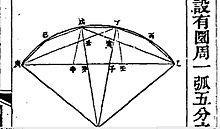五分弦

几何意义：

。

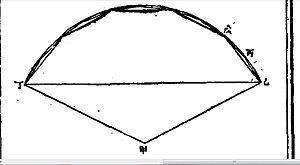十分弦图

从十分弦开始，明安图不再作几何模型，而是对无穷级数进行代数运算

显然十分弦等于五分弦和二分弦的组合，即

;

展开即得：

+……。

同理，

,展开后即得：

……。

……。

…………。

y100,y1000 and y10000 可表为:

..........

..............

..................

分弦数越大，分母24.000000240000002400、24.000002400000218400*80越接近24 、 24*80 ；当分弦数n趋向无穷大， n*a, 就变成 弧背，于是

令c 为弦，a 为弧背，

.....

明安图求得上述无穷级数的反逆，将弧表示为弦的无穷级数:

............

,

令 r=1

…………

。