相位谱

信号的相位谱和信号的幅度谱一样，是^[1]信号的重要特征之一。讨论相位谱的特点和性质是信号谱分析的一个基本问题，尤其是在多点激励、载荷建立以及传递路径识别等方面问题的研究中，相位谱起着重要的作用。

相位谱是调整声音相位的，最容易理解的就是左右声道的位置调整，实际上相位还决定着其他很多声音的属性。

对于一个系统，能够通过其相位谱来判断该系统是否为线性相位系统。线性相位系统故名思义，看相位是否随频率线性变化。但相位谱的作用不仅限于此，奥本海姆在一篇经典文献中认为信号的相位包含的信息大于幅度，实际上从最初的最小相位系统，倒谱分析，到系统辨识，高阶谱估计等理论都是以相位谱为突破口。

对于某一个固定的模型，其相位值随频率的变化就称为相位谱。傅里叶变换可实现时频转换，时间域的观测成果转换到频率域，就有了相位。频率趋于“0”和无限大时，相位趋于“0”，而在某一频率，相频特性曲线有峰值。
利用此特点，有可能区分极化体性质。

傅里叶变换

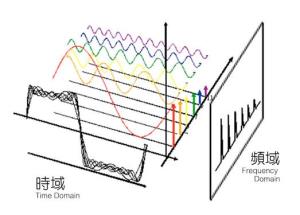傅立叶变换是^[2]数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义，首先要了解傅立叶原理的意义。傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

线性相位是指滤波器的相位响应是^[3]频率的线性函数（在+/-180度）。因此滤波器的延时后，所有的频率相位相同。因而滤波器不会产生相位和延迟扭曲。在某些领域，比如数字解调器，没有相位或者延迟扭曲是FIR滤波器相对于其他IIR和模拟滤波器的一个关键优点。

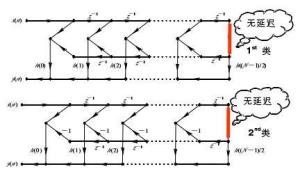一个单一频率的正弦信号通过一个系统，假设它通过这个系统的时间需要t，则这个信号的输出相位落后原来信号wt的相位。从这边可以看出，一个正弦信号通过一个系统落后的相位等于它的w*t；

反过来说，如果一个频率为w的正弦信号通过系统后，它的相位落后delta，则该信号被延迟了delta/w的时间。在实际系统中，一个输入信号可以分解为多个正弦信号的叠加，为了使得输出信号不会产生相位失真，必须要求它所包含的这些正弦信号通过系统的时间是一样的。因此每一个正弦信号的相位分别落后，w1*t，w2*t，w3*t。

因此，落后的相位正比于频率w，如果超前，超前相位的大小也是正比于频率w。从系统的频率响应来看，就是要求它的相频特性是一条直线。在FIR滤波器的设计中，为了得到线性相位的性质，通常利用实偶对称序列的相频特性为常数0和实奇对称序列为相频特性为常数90度的特点。因此得到的是对称序列，不是因果序列，是不可实现系统，为了称为物理可实现系统，需要将它向右移动半个周期，这就造成了相移特性随时间的变化，同时也是线性变化。

即如果单位脉冲响应h(n)（为实数）具有偶对称或奇对称性，则FIR数字滤波器具有严格的线性相位特性。 数字滤波器中，IIR数字滤波器方便简单，但它相位的非线性，要求采用全通网络进行相位校正，且稳定性难以保障。FIR滤波器具有很好的线性相位特性，使得它越来越受到广泛的重视。