三力平衡

三力平衡　　如果一个物体受到三个力的作用也能处于平衡状态，叫做三力平衡。很显然这三个力的合力应该为零。而这三个力可能互成角度，也可能在一条直线上。物体在三个力的作用下处于平衡状态，要求我们分析三力之间的相互关系的问题叫三力平衡问题，这是物体受力平衡中最重要、最典型也最基础的平衡问题。

三力平衡汇交定理：当物体受到同平面内不平行的三力作用而平衡时，三力的作用线必汇交于一点。即物体在互相不平行的三个力作用下处于平衡状态时，这三个力必定共面共点，合力为零。

弱定理：刚体受三个互不平行但共面的力作用而平衡时，这三个力的作用线必汇交于一点。

强定理：作用于物体上的三个相互平衡、但又不互相平行的力，若其中两个力的作用线汇交于一点， 则此三力必在同一个平面内，且第三个力的作用线通过前两个力的汇交点。^[1]

物体在几个共点力作用下处于静止状态或匀速直线运动状态，作用在物体上的这几个力的合力为零。若物体在三个共点力的作用下处于静止或匀速直线运动状态，这三个力的合力必为零，此时可运用三角形法则进行分析与求解。

三个共点力的合力为零时，若用平行四边形定则求出任意两力的合力，这个合力将代替原来的两个力，这样，三力平衡问题就变成了二力平衡问题，合力与第三个力大小相等、方向相反、作用在同一条直线上。因此，若将表示三个力的矢量平行移动，使其依次首尾相接，将构成封闭三角形。这就是求解与分析三个共点力平衡问题的三角形法则。运用三角形法则作出表示力矢量的三角形后，可利用解三角形的知识与方法进行分析与求解。^[2]

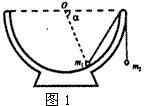
例1．如图1所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的。一根细线

图1

跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α＝60°。则小球的质量比m2/m1为

解析：选碗中的小球m1为研究对象，如图2所示，由于碗的内表面光滑，它受竖直向下的重力mg、从m1（质点）

图2、3

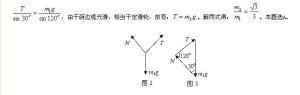
指向球心O的支持力N（弹力）、沿细线斜向上的拉力T（弹力）三个力的作用而处于静止状态，由力的平衡条件可知，它们的合力为零，故将表示这三个力的矢量平行移动依次首尾相接，将构成封闭三角形，如图3所示。由正弦定理有：

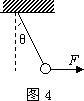图4物体在三个共点力的作用下处于静止状态或匀速直线运动状态，若其中的一个力缓慢变化，而物体仍处于静止状态或匀速直线运动状态，这类问题就是动态平衡问题，变力变化过程中的每一个状态，三力的合力都等于零。这类问题中至少有一个大小、方向均保持不变，三力矢量构成的封闭三角形中，至少有一个边保持不变，即三角形的两个顶点将保持不动，根据题中变力的变化情况，可确定出另一顶点的变化，由此可以判断出变力的变化情况。

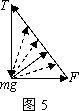图5例2．如图5所示，质量为m的小球用细线悬于天花板上。在小球上作用水平拉力F，使细线与竖直方向保持θ角，小球保持静止状态。现让力F缓慢由水平方向变为竖直方向。这一过程中，小球处于静止状态，细线与竖直方向夹角不变。则力F的大小、细线对小球的拉力大小如何变化？

解析：由于小球始终保持静止状态，小球受的重力mg、水平拉力F和细线拉力T三个矢量将组成封闭三角形，如图5所示。由于重力mg大小及方向均不变，三角形的两个顶点（矢量mg的首尾）固定不动；由于θ角保持不变，即表示细线拉力T的边方向不变，当F由水平逐渐变竖直时，力矢量F与力矢量T的交点，三角形的另一顶点将沿矢量T逐渐向上滑移，由图可以看出表示力矢量F的边先是逐渐变小，当与细线垂直时有最小值，接着逐渐变大。这一过程中，表示细线拉力T的边一直减小到零。

故，力F先逐渐减小再逐渐增大，细线的拉力一直减小。

对于三力平衡，一般根据“任意两个力的合力与第三个力等大反向”的关系，借助三角函数、相似三角形等手段求解；或将某一个力分解到另外两个力的反方向上，得到的这两个分力势必与另外两个力等大、反向；对于多个力的平衡，利用先分解再合成的正交分解法。

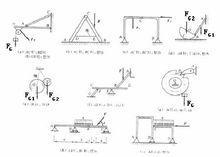三力平衡① 三个力中，有两个力互相垂直，第三个力角度（方向）已知。

② 三个力互相不垂直，但夹角（方向）已知《考试说明》中规定力的合成与分解的计算只限于两力之间能构成直角的情形。三个力互相不垂直时，无论是用合成法还是分解法，三力组成的三角形都不是直角三角形，造成求解困难。因而这种类型问题的解题障碍就在于怎样确定研究方法上。解决的办法是采用正交分解法，将三个不同方向的力分解到两个互相垂直的方向上，再利用平衡条件求解。

③ 三个力互相不垂直，且夹角（方向）未知

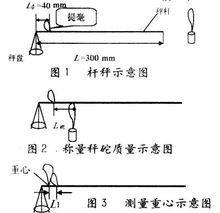老式杆秤三力方向未知时，无论是用合成法还是分解法，都找不到合力与分力之间的定量联系，因而单从受力分析图去求解这类问题是很难找到答案的。要求解这类问题，必须变换数学分析的角度，从我们熟悉的三角函数法变换到空间几何关系上去考虑，因而这种问题的障碍点是如何正确选取数学分析的方法。

解决这种类型的问题的对策是：首先利用合成法或分解法作出三力之间的平行四边形关系和三角形关系，再根据力的三角形寻找与之相似的空间三角形，利用三角形的相似比求解。

④ 三力的动态平衡问题

即三个力中，有一个力为恒力，另一个力方向不变，大小可变，第三个力大小方向均可变，分析第三个力的方向变化引起的物体受力的动态变化问题。^[3]

这种类型的问题不需要通过具体的运算来得出结论，因而障碍常出现在受力分析和画受力分析图上。在分析这类问题时，要注意物体“变中有不变”的平衡特点，在变中寻找不变量。即将两个发生变化的力进行合成，利用它们的合力为恒力的特点进行分析。在解决这类问题时，正确画出物体在不同状态时的受力图和平行四边形关系尤为重要。