- 空间直角坐标变换

空间直角坐标变换
基本介绍
在用坐标法讨论变形的时候,首要的问题是选取一个适当的坐标系来化简问题,并且常常需要把一个坐标系中的结果转化到另一个坐标系中去。要解决这个问题,最基本的是求出同一个点在两个不同的坐标系中的坐标变换公式。
设在空间给出了两个右手直角坐标系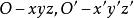 ,
,![]() 和
和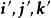 分别是两组坐标基向量,它们是空间中的两组标准正交基。前一个称为旧坐标系,后一个坐标系称为新坐标系。它们之间的位置关系完全可以由新坐标系的原点在旧坐标系中的坐标,以及新坐标系的坐标向量在旧坐标系中的坐标所决定。下面先讨论直角坐标系的移轴和转轴(也称为平移和旋转),然后通过移轴和转轴给出直角坐标变换的一般公式[1]。
分别是两组坐标基向量,它们是空间中的两组标准正交基。前一个称为旧坐标系,后一个坐标系称为新坐标系。它们之间的位置关系完全可以由新坐标系的原点在旧坐标系中的坐标,以及新坐标系的坐标向量在旧坐标系中的坐标所决定。下面先讨论直角坐标系的移轴和转轴(也称为平移和旋转),然后通过移轴和转轴给出直角坐标变换的一般公式[1]。
移轴变换
设坐标系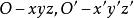 的原点
的原点![]() 不同,
不同,![]() 在旧坐标系中的坐标为
在旧坐标系中的坐标为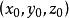 ,但是坐标基向量相同
,但是坐标基向量相同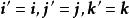 ,这时新坐标系可以看成由
,这时新坐标系可以看成由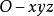 平移到使
平移到使![]() 重合而得(如图1所示),这种坐标变换称为移轴变换[1]。
重合而得(如图1所示),这种坐标变换称为移轴变换[1]。
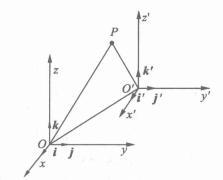 图1
图1
现在推导移轴变换公式,设P为空间任意一点,它在坐标系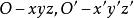 中的坐标分别是
中的坐标分别是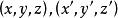 ,则有
,则有
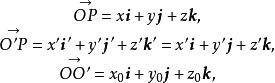 又
又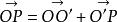 ,代入得
,代入得
![]() 所以
所以
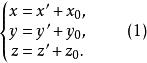
这就是空间直角坐标系的移轴公式。
从(1)解出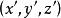 ,就得到移轴的逆变换公式
,就得到移轴的逆变换公式
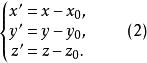
转轴变换
设两个右手坐标系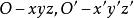 的原点相同,但坐标向量
的原点相同,但坐标向量![]() 和
和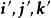 不同,这时新坐标系可以看成由旧坐标系绕原点旋转,使得
不同,这时新坐标系可以看成由旧坐标系绕原点旋转,使得![]() 分别与
分别与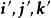 重合得到的(如图2所示),这种坐标变换称为转轴变换[1]。
重合得到的(如图2所示),这种坐标变换称为转轴变换[1]。
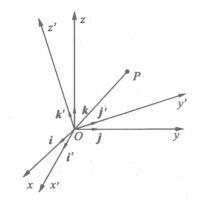 图2
图2
下面推导转轴变换公式,具有相同原点的两坐标系之间的位置关系完全由新、旧坐标轴之间的夹角来决定见表1。![]() 轴
轴![]()
![]() 轴
轴![]() ,,,
,,,![]() 轴
轴![]()
![]() 轴
轴![]()
![]() 轴
轴![]()
| α1 | β1 | γ1 | |
| α2 | β2 | γ2 | |
| α3 | β3 | γ3 |
由于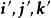 都是单位向量,其坐标为它的3个方向余弦。故从表1可知
都是单位向量,其坐标为它的3个方向余弦。故从表1可知

设空间任意一点P在旧坐标系中的坐标为![]() ,在新坐标系中的坐标为
,在新坐标系中的坐标为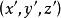 ,那么有
,那么有
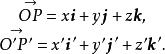
由于![]() ,由上面两式得:
,由上面两式得:
![]()
将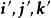 代人得
代人得
![]()
![]() 于是有
于是有
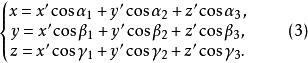 这就是空间直角坐标变换的转轴公式。注意
这就是空间直角坐标变换的转轴公式。注意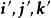 在旧坐标系的坐标为(3)中的各列系数(行变列)。转轴的逆变换公式为[1]
在旧坐标系的坐标为(3)中的各列系数(行变列)。转轴的逆变换公式为[1]
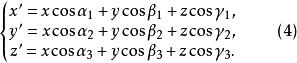
正交条件
| α1 | β1 | γ1 | |
| α2 | β2 | γ2 | |
| α3 | β3 | γ3 |

-
实拍江铃新宝典(图文) 空间满足家用
2025-10-31 18:37:00 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-10-31 18:37:00 查看详情 -
江铃福特轻客持续打造最优TCO 空间满足家用
2025-10-31 18:37:00 查看详情 -
航天恒星空间技术应用有限公司
2025-10-31 18:37:00 查看详情


 求购
求购





