- 希尔排序

希尔排序
基础定义
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止
历史沿革
希尔排序按其设计者希尔(Donald Shell)的名字命名,该算法由1959年公布。一些老版本教科书和参考手册把该算法命名为Shell-Metzner,即包含Marlene Metzner Norton的名字,但是根据Metzner本人的说法,“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。”
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
1961年,IBM 公司的女程序员 Marlene Metzner Norton(玛琳·梅茨纳·诺顿)首次使用 FORTRAN 语言编程实现了希尔排序算法。在其程序中使用了一种简易有效的方法设置希尔排序所需的增量序列:第一个增量取待排序记录个数的一半,然后逐次减半,最后一个增量为 1。该算法后来被称为 Shell-Metzner 算法,Metzner 本人在2003年的一封电子邮件中说道:“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。[3]
基本思想
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量![]() =1(
=1(![]() <
<![]() …<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
该方法实质上是一种分组插入方法
比较相隔较远距离(称为增量)的数,使得数移动时能跨过多个元素,则进行一次比较就可能消除多个元素交换。D.L.shell于1959年在以他名字命名的排序算法中实现了这一思想。算法先将要排序的一组数按某个增量d分成若干组,每组中记录的下标相差d.对每组中全部元素进行排序,然后再用一个较小的增量对它进行,在每组中再进行排序。当增量减到1时,整个要排序的数被分成一组,排序完成。
一般的初次取序列的一半为增量,以后每次减半,直到增量为1。
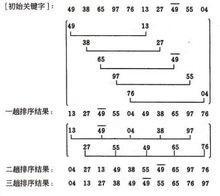
给定实例的shell排序的排序过程
假设待排序文件有10个记录,其关键字分别是:
49,38,65,97,76,13,27,49,55,04。
增量序列的取值依次为:
5,2,1
 希尔排序
希尔排序
稳定性
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
排序过程
缩小增量
希尔排序属于插入类排序,是将整个有序序列分割成若干小的子序列分别进行插入排序。
排序过程:先取一个正整数d1<n,把所有序号相隔d1的数组元素放一组,组内进行直接插入排序;然后取d2<d1,重复上述分组和排序操作;直至di=1,即所有记录放进一个组中排序为止。
三趟结果
04 13 27 38 49 49 55 65 76 97
Shell排序
Shell排序的算法实现:
1. 不设监视哨的算法描述
void ShellPass(SeqList R,int d)//希尔排序中的一趟排序,d为当前增量 {
for(i=d+1;i<=n;i++)//将R[d+1..n]分别插入各组当前的有序区
if(R[ i ].key0&&R[0].key算法分析
优劣
不需要大量的辅助空间,和归并排序一样容易实现。希尔排序是基于插入排序的一种算法, 在此算法基础之上增加了一个新的特性,提高了效率。希尔排序的时间复杂度与增量序列的选取有关,例如希尔增量时间复杂度为O(n²),而Hibbard增量的希尔排序的时间复杂度为O(![]() ),希尔排序时间复杂度的下界是n*log2n。希尔排序没有快速排序算法快 O(n(logn)),因此中等大小规模表现良好,对规模非常大的数据排序不是最优选择。但是比O(
),希尔排序时间复杂度的下界是n*log2n。希尔排序没有快速排序算法快 O(n(logn)),因此中等大小规模表现良好,对规模非常大的数据排序不是最优选择。但是比O(![]() )复杂度的算法快得多。并且希尔排序非常容易实现,算法代码短而简单。 此外,希尔算法在最坏的情况下和平均情况下执行效率相差不是很多,与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡,几乎任何排序工作在开始时都可以用希尔排序,若在实际使用中证明它不够快,再改成快速排序这样更高级的排序算法. 本质上讲,希尔排序算法是直接插入排序算法的一种改进,减少了其复制的次数,速度要快很多。 原因是,当n值很大时数据项每一趟排序需要移动的个数很少,但数据项的距离很长。当n值减小时每一趟需要移动的数据增多,此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。Shell算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列,可以准确地估算关键词的比较次数和对象移动次数。想要弄清关键词比较次数和记录移动次数与增量选择之间的关系,并给出完整的数学分析,今仍然是数学难题。
)复杂度的算法快得多。并且希尔排序非常容易实现,算法代码短而简单。 此外,希尔算法在最坏的情况下和平均情况下执行效率相差不是很多,与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡,几乎任何排序工作在开始时都可以用希尔排序,若在实际使用中证明它不够快,再改成快速排序这样更高级的排序算法. 本质上讲,希尔排序算法是直接插入排序算法的一种改进,减少了其复制的次数,速度要快很多。 原因是,当n值很大时数据项每一趟排序需要移动的个数很少,但数据项的距离很长。当n值减小时每一趟需要移动的数据增多,此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。Shell算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列,可以准确地估算关键词的比较次数和对象移动次数。想要弄清关键词比较次数和记录移动次数与增量选择之间的关系,并给出完整的数学分析,今仍然是数学难题。
时间性能
1.增量序列的选择
Shell排序的执行时间依赖于增量序列。
好的增量序列的共同特征:
① 最后一个增量必须为1;
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
有人通过大量的实验,给出了较好的结果:当n较大时,比较和移动的次数约在nl.25到1.6n1.25之间。
2.Shell排序的时间性能优于直接插入排序
希尔排序的时间性能优于直接插入排序的原因:
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时,n和![]() 的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(
的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(![]() )差别不大。
)差别不大。
③在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快,后来增量di逐渐缩小,分组数逐渐减少,而各组的记录数目逐渐增多,但由于已经按di-1作为距离排过序,使文件较接近于有序状态,所以新的一趟排序过程也较快。
因此,希尔排序在效率上较直接插入排序有较大的改进。
希尔分析
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小,插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比o(n^2)好一些。
代码实现
JAVA
public static void main(String[] args){
int[] array={49,38,65,97,76,13,27,49,78,34,12,64,1};
System.out.println("排序之前:");
for(int i=0;i<="" j="i" temp="array[j];" k="" -="">= 0 && array[k] > temp) {
array[k + gap] = array[k];
k -= gap;
}
array[k + gap] = temp;
}
}
if (gap == 1)
break;
}
System.out.println();
System.out.println("排序之后:");
for(int i=0;i伪代码
input: an array a of length n with array elements numbered 0 to n − 1
inc ← round(n/2)
while inc > 0 do:
for i = inc .. n − 1 do:
temp ← a[i]
j ← i
while j ≥ inc and a[j − inc] > temp do:
a[j] ← a[j − inc]
j ← j − inc
a[j] ← temp
inc ← round(inc / 2.2)Golang
| 12345678910111213 | func ShellSort(nums []int) []int{ //外层步长控制 for step := len(nums) / 2; step > 0; step /= 2 { //开始插入排序 for i := step; i < len(nums); i += step { //满足条件则插入 for j := i - step; j >= 0 && nums[j+step] < nums[j]; j -= step { nums[j], nums[j+step] = nums[j+step], nums[j] } } } return nums} |
vb.net
| 12345678910111213141516 | Function Shell(Byval lines() As Integer) As Integer() dim c() As Integer=lines.clone,div,i,j,k As Integer,Data As Integer if UBound(c)=1 then return lines For div=len/2 To 1 div/=2 For i=0 To div Step 1 For j=i To len-div For k=j to len Step div If(data[j]>data[k]) swapInt(data+j,data+k) End If Next Next Next NextEnd Function |
javascript
| 123456789101112 | var arr = [49, 38, 65, 97, 76, 13, 27, 49, 55, 04];var len = arr.length;for (var fraction = Math.floor(len / 2); fraction > 0; fraction = Math.floor(fraction / 2)) { for (var i = fraction; i <= len; i += fraction) { for (var j = i - fraction; j >= 0 && arr[j] > arr[fraction + j]; j -= fraction) { var temp = arr[j]; arr[j] = arr[fraction + j]; arr[fraction + j] = temp; } }}console.log(arr); |
pascal
| 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051 | const size=12;type arr=array[1..size]ofinteger;var a:arr; i,j,k,t:integer;procedure DataInput;//生成随机数列begin randomize; for i:=1 to size do begin a[i]:=random(99)+1; write(a[i]:3); end; writeln; end;procedure DataOutput;//输出begin for i:=1 to size do write(a[i]:3); end;procedure insertionsort(var a:arr);begin for i:=2 to size do begin t:=a[i]; j:=i-1; while (j>0) and (t<a[j]) do begin a[j+1]:=a[j]; j:=j-1; end; a[j+1]:=t; end;end;begin DataInput; k:=size; while k>1 do begin k:=k div 2; for j:=k+1 to size do begin t:=a[j]; i:=j-k; while (i>0) and (a[i]>t) do begin a[i+k]:=a[i]; i:=i-k; end; a[i+k]:=t; end; end; DataOutput;end. |
Kotlin
| 123456789101112131415 | fun sort(arr: IntArray) { var gap = arr.size / 2 while (1 <= gap) { for (i in gap..arr.size - 1) { var j = i - gap val tmp = arr[i] while (j >= 0 && tmp < arr[j]) { arr[j + gap] = arr[j] j -= gap } arr[j + gap] = tmp } gap /= 2 }} |
C#
| 12345678910111213141516171819202122232425262728293031 | using System;using System.Collections.Generic; namespace Demo{ class Program { public static List<int> ShellSort(List<int> data) { for (int gap = data.Count / 2; gap > 0; gap = gap / 2) { for (var i = gap; i < data.Count; i++) { var j = i; var current = data[i]; while (j - gap >= 0 && current < data[j - gap]) { data[j] = data[j - gap]; j = j - gap; } data[j] = current; } } return data; } public static void Main(String[] args) { var iArray = new List<int> { 1, 5, 3, 6, 10, 55, 55, 100, 9, 2, 87, 12, 34, 75, 33, 47 }; var newArray = ShellSort(iArray); Console.WriteLine(string.Join(",", newArray)); } }} |
C语言
| 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748 | #include<stdio.h>#include<math.h> #define MAXNUM 10 void shellSort(int array[],int n,int t);//t为排序趟数 void main(){ int array[MAXNUM],i; for(i=0;i<MAXNUM;i++) scanf("%d",&array[i]); shellSort(array,MAXNUM,(int)(log(MAXNUM+1)/log(2)));//排序趟数应为log2(n+1)的整数部分 for(i=0;i<MAXNUM;i++) printf("%d ",array[i]); printf("\n");} //根据当前增量进行插入排序void shellInsert(int array[],int n,int dk){ int i,j,temp; for(i=dk;i<n;i++)//分别向每组的有序区域插入 { temp=array[i]; for(j=i-dk;(j>=i%dk)&&array[j]>temp;j-=dk)//比较与记录后移同时进行 array[j+dk]=array[j]; if(j!=i-dk) array[j+dk]=temp;//插入 }} //计算Hibbard增量int dkHibbard(int t,int k){ return (int)(pow(2,t-k+1)-1);} //希尔排序void shellSort(int array[],int n,int t){ void shellInsert(int array[],int n,int dk); int i; for(i=1;i<=t;i++) shellInsert(array,n,dkHibbard(t,i));} //此写法便于理解,实际应用时应将上述三个函数写成一个函数。 |
C++
| 123456789101112131415 | template <typename _RIter>void insert_sort(_RIter st, _RIter ed, int delta) { for(_RIter i = st + delta; i < ed; i += delta) { for(_RIter j = i; j > st; j -= delta) if(*j < *(j - delta)) std::swap(*j, *(j - delta)); else break; }} template <typename _RIter>void shell_sort(_RIter st, _RIter ed) { for(int delta = ed - st; delta; delta /= 2) for(int i = 0; i < delta; i++) insert_sort(st + i, ed, delta);} |
AS3
| 123456789101112131415161718 | //需要排序的数组var arr:Array = [7, 5, 8, 4, 0, 9];var small:int;//最小下标var temp:int;for(var i:int = 0; i < arr.length; i++){ small = i; for(var j:int = i + 1; j < arr.length + 1; j++){ if(arr[j] < arr[small]){ small = j; } } if(small != i){ temp = arr[i]; arr[i] = arr[small]; arr[small] = temp; } trace(arr[i]);} |
Ruby
| 1234567891011121314 | def shell_sort(array) gap = array.size while gap > 1 gap = gap / 2 (gap..array.size-1).each do |i| j = i while j > 0 array[j], array[j-gap] = array[j-gap], array[j] if array[j] <= array[j-gap] j -= gap end end end arrayend |
PHP
| 12345678910111213 | function shell_sort(&$arr) { if(!is_array($arr)) return; $n = count($arr); for ($gap = floor($n/2); $gap > 0; $gap = floor($gap/=2)) { for($i = $gap; $i < $n; ++$i) { for($j = $i - $gap; $j >= 0 && $arr[$j + $gap] < $arr[$j]; $j -= $gap) { $temp = $arr[$j]; $arr[$j] = $arr[$j + $gap]; $arr[$j + $gap] = $temp; } } }} |
Python3.x
| 1234567891011121314151617181920212223 | def shell_sort(seq): """ 希尔排序 思想:通过控制增量将序列分组,组内直接插入排序完再缩小增量再分组排序, 如8个序列,最初增量为8/2=4,所以1~4为一组,5~8为一组,1-5比较、2-6比较、 3-7比较、4-8比较,此时组内比较再增量/2分组,直到最后增量为1时排序次数就少很多 :param seq: 待排序的序列 :return: """ seq_len = len(seq) step = seq_len >> 1 # 增量小于1说明最终排序已完成 while step: for i in range(step, seq_len): # j记录元素原始位置,用于查找前面所有小于当前元素的元素 j = i while seq[j] < seq[j-step] and j-step >= 0: seq[j], seq[j-step] = seq[j-step], seq[j] # 改变下标,查看前面是否还有更小的值 j -= step print(f"增量{step}的排序:", seq) # 每次增长减小一半 step = step >> 1 |
Objective-C
| 1234567891011121314 | + (NSArray *)shellSort:(NSArray *)unsortDatas { NSMutableArray *unSortArray = [unsortDatas mutableCopy]; int len = (int)unSortArray.count; for (int gap = floor(len / 2); gap > 0; gap = floor(gap/2)) { for (int i = gap; i < len; i++) { for (int j = i - gap; j >= 0 && [unSortArray[j] integerValue] > [unSortArray[j+gap] integerValue]; j-=gap) { NSNumber *temp = unSortArray[j]; unSortArray[j] = unSortArray[gap+j]; unSortArray[gap+j] = temp; } } } return [unSortArray copy];} |
Rust
| 1234567891011121314151617181920212223 | pub fn shell_sort(nums:&Vec<i32>)->Vec<i32>{ let mut nums = nums.to_vec(); fn insertion(nums: &mut Vec<i32>, start: usize, gap: usize) { for i in ((start + gap)..nums.len()).step_by(gap) { let val_current = nums[i]; let mut pos = i; // make swaps while pos >= gap && nums[pos - gap] > val_current { nums[pos] = nums[pos - gap]; pos = pos - gap; } nums[pos] = val_current; } } let mut count_sublist = nums.len() / 2; // makes gap as long as half of the array while count_sublist > 0 { for pos_start in 0..count_sublist { insertion(&mut nums, pos_start, count_sublist); } count_sublist /= 2; // makes gap as half of previous } return nums} |
词条图册
| 12345678910111213 | func ShellSort(nums []int) []int{ //外层步长控制 for step := len(nums) / 2; step > 0; step /= 2 { //开始插入排序 for i := step; i < len(nums); i += step { //满足条件则插入 for j := i - step; j >= 0 && nums[j+step] < nums[j]; j -= step { nums[j], nums[j+step] = nums[j+step], nums[j] } } } return nums} |

-
重庆希尔安药业有限公司
2025-11-02 18:40:50 查看详情


 求购
求购








