- 分数阶微积分

分数阶微积分
分数阶微积分定义
在这个上下文中,幂指数反复使用,和
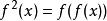
中的平方意义相同。例如,可以提出如何解释如下符号的问题
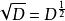
作为微分算子的平方根(半次操作),也就是一种算子操作两次以后可以有微分的效果。
更一般的,
![]()
对于实数值的n,使得当n为整数时,若n>0,它等同于通常的幂n次操作,当n<0,它等同于n次积分J。
讨论这个问题有几个原因。一个是,这样幂D组成的半群可以看作一个连续的半群中取离散值的部分。连续半群在数学上有很好的研究,有一个有趣的理论。注意,分数是个错误的记号,因为指数可以取非有理数,但是分数微积分已成为习惯用法。
试探法
一个很自然的想法是问,是否存在一个算子![]() 起到半导数的作用,即使得:
起到半导数的作用,即使得:
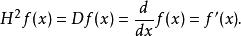
结论是:这样的算子是存在的,对于任意![]() ,存在一个算子
,存在一个算子![]() ,满足:
,满足:
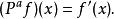
或者换一个说法,![]() 的定义可以从正整数n扩充到所有的实数n.
的定义可以从正整数n扩充到所有的实数n.
在这里我们引入Γ函数将阶乘扩展到实数和复数域上.Γ函数的定义如下:
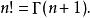
假设对函数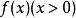 在0到x上求积分,我们可以形式的定义积分算子J:
在0到x上求积分,我们可以形式的定义积分算子J:
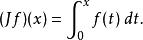
重复这个过程,可得:
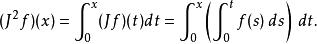
这个过程可以任意的重复下去。
利用重复积分的柯西公式,即:
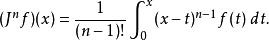
我们可以直截了当的写出任意实数n的积分算子。
直接利用![]() 函数将离散的阶乘扩展为连续的函数。我们可以自然的得到分数积分算子的表达形式
函数将离散的阶乘扩展为连续的函数。我们可以自然的得到分数积分算子的表达形式
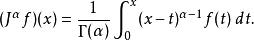
这个算子定义明确而且具有良好的性质。
可以证明J算子满足如下关系
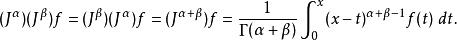
这个性质叫微分积分算符的半群性。然而用类似方法定义微分算子将变得相当困难,而且定义出来的微分算子D一般来说不对易也不具有叠加性。
分数微分在一个简单函数上的应用
这个动画展示了不同分数微分算子如何操作在y=x(蓝色),结果(绿色)在一般的积分(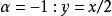 ,紫色)及一般的一次微分(
,紫色)及一般的一次微分(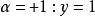 ,红色)间连续变化。
,红色)间连续变化。
假设有一个函数
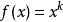 。它的一阶导数一般是:
。它的一阶导数一般是:
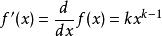 。重复这一过程,得到更一般的结果:
。重复这一过程,得到更一般的结果:
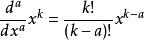 ,将阶乘用伽玛函数替换,可得:
,将阶乘用伽玛函数替换,可得:
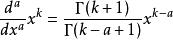 。当k = 1,并且a = 1/2时我们可以得到函数
。当k = 1,并且a = 1/2时我们可以得到函数![]() 的半导数:
的半导数:
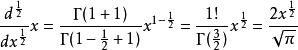 。重复这一过程,得:
。重复这一过程,得:
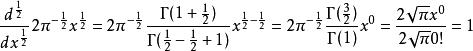 ,这正是期望的结果:
,这正是期望的结果:
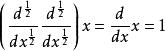 。
。
以上微分算子的扩展不仅仅局限于实数次。举个例子,![]() 阶导数作用后,
阶导数作用后,![]() 阶导数再作用,可以得到二阶导数。同时如果a为负则可为求积分。
阶导数再作用,可以得到二阶导数。同时如果a为负则可为求积分。
分数微分可以得到上述相同的结果(当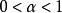 )。
)。
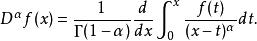
对于任意的![]() ,由于伽玛函数的参数在实数部为负整数时没有定义,需要在分数微分前先进行整数微分。例如
,由于伽玛函数的参数在实数部为负整数时没有定义,需要在分数微分前先进行整数微分。例如
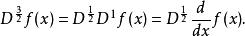
应用
WKB近似
对于一个一维的量子系统进行准经典的近似时,系统哈密顿量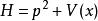 中
中![]() 的倒数
的倒数![]() 可由对态密度的半阶微分求出
可由对态密度的半阶微分求出
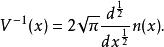
这里采用了自然单位制,即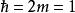 。
。

-
长城汽车蜂巢传动邳州基地投产 长城发布自主首个高阶动力总成
2025-11-02 12:43:13 查看详情 -
长城炮全新车型将于成都车展首发 长城发布自主首个高阶动力总成
2025-11-02 12:43:13 查看详情 -
长城山海炮开启量产 长城发布自主首个高阶动力总成
2025-11-02 12:43:13 查看详情 -
比例积分电动三通调节阀
2025-11-02 12:43:13 查看详情 -
加油卡怎么使用(邮政积分兑换加油卡怎么使用)
2025-11-02 12:43:13 查看详情 -
梅赛德斯 公开部分数据/技术源自F1
2025-11-02 12:43:13 查看详情


 求购
求购



