盈数

盈数（又称 丰数， 过剩数abundant number)是一种特殊的 自然数，除去它本身以外的一切正约数的和大于它本身。

最小的一些过剩数是： 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, … 

以上列出的盈数都是 偶数。最小的盈奇数是945。

与盈数数相关的概念是 完全数（ ( ) = 2 ）和 亏数（ ( ) < 2 ）。最早将自然数分为盈数、完美数和亏数的是Nicomachus所著的Introductio Arithmetica (公元前100年)。

1998年Marc Deléglise 证明了盈数在自然数中的自然密度介于0.2474 与0.2480之间。

奇盈数和偶盈数都有无穷多个，因为每个 完全数和盈数的倍数（不包括它们自身）都是盈数。甚至，每个大于20161的数都可以写成两个盈数之和。许多盈数一部分真约数的和等于盈数自身，这样的盈数也是 半完全数，一个不是半完美数的盈数叫做 奇异数；盈度为1的盈数叫做准完全数。

假定有一正整数n，其所有正整数因子的和为m（例如，若n为12，则其和为1+2+3+4+6=16），则正整数n必有以下三种情形：

m <2n 亏数(deficient number) 1,2,3,4,5,7,8,9 ...

m =2n 完美数( 完全数，perfect number) 6,28,496 ...

m >2n 盈数(abundant number) 12,18,20,24,30 ...

最早这么命名亏数和盈数的是Nicomachus所著的Introductio Arithmetica (公元前100年)。

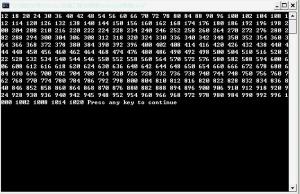最小的一些过剩数是： 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, …（ OEIS中的数列 A005101）

以上列出的过剩数都是 偶数。最小的奇过剩数是945。

奇过剩数和偶过剩数都有无穷多个，因为每个 完美数和过剩数的倍数（不包括它们自身）都是过剩数。甚至，每个大于20161的数都可以写成两个过剩数之和。许多过剩数一部分真因子的和等于过剩数自身，这样的过剩数也是半完美数，一个不是半完美数的过剩数叫做 奇异数；盈度为1的过剩数叫做准完美数。每一完美数的完全倍数以及每一盈数的倍数都是盈数(因为，当n>1时，σ(n)/n >1+1/n；且σ(n) 为 积性函数multiplicative function，即n的所有正因子之和)。1998年Marc Deléglise 证明了过剩数在自然数中的自然密度介于0.2474 与0.2480之间。

每一大于20161的整数可写成两个过剩数之和。

半完全数全部都是过剩数（盈数）。