- radon变换

radon变换
中文名
radon变换
对应
原始函数的某个线积分值
按照
合适的角度
简介
若函数F表示一个未知的密度,对F做radon变换,相当于得到F投影后的讯号,举例来说:F相当于人体组织,断层扫描的输出讯号相当于经过radon变换的F。 因此,可以用radon反变换从投影后的密度函数,重建原始的密度函数,它也是重建断层扫描的数学理论基础,另一个被广为人知名词的是三维重建[1]。
radon变换后的讯号称作“正弦图”,因为一个偏离中心的点的radon变换是一个正弦曲线。所以对一些小点的radon变换,会看起来像很多不同振福、相位的正弦函数重叠在一起。
定义
令密度函数f(X)=f(x,y)是一个的定义域为R2的紧致台(compact support)。令R为radon变换的运算子,则Rf(x,y)是一个定义在R2空间中的直线L,它的定义如下[1]:
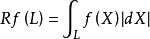
应用
radon变换可以应用在:X射线电脑断层扫描、条码扫描器、蛋白质复合体,而且也是双曲线偏微分方程的解。

相关百科
-
PRO上市 售价9.48万
2025-10-31 18:27:02 查看详情 -
长安凯程GDI双侠成都上市 或将于下半年上市
2025-10-31 18:27:02 查看详情 -
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-10-31 18:27:02 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-10-31 18:27:02 查看详情 -
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-10-31 18:27:02 查看详情 -
实拍江铃福特Equator 创富之选
2025-10-31 18:27:02 查看详情 -
实拍江铃福特Equator 江铃福特领界上市怎么选
2025-10-31 18:27:02 查看详情 -
Pro将于4月15日上市 12.9万元
2025-10-31 18:27:02 查看详情 -
捷途X95热爱Pro版上市 别克微蓝6插混车型上市
2025-10-31 18:27:02 查看详情 -
比亚迪秦Pro超越版将于5月20日上市 售价33900元
2025-10-31 18:27:02 查看详情


 求购
求购

