- 正十七边形

正十七边形
基础定义
正十七边形,是指几何学中有17条边及17只角的正多边形。正十七边形的每个内角约为158.8235294117647°,其内角和为2700°,有119条对角线。最早发现其形状可用尺规作图法作出的是高斯。
演绎过程
 正十七边形最早的十七边形画法创造人是高斯【1801年数学家高斯证明:如果费马数k为质数,那么,就可以用直尺和圆规将圆周k等分。但是,高斯本人并没有用尺规做出正十七边形,事实上,完成证明之后正十七边形的做法对数学研究者是显而易见的。第一个真正的正十七边形尺规作图法是在1825年由约翰尼斯·厄钦格(Johannes Erchinger)给出.】。
正十七边形最早的十七边形画法创造人是高斯【1801年数学家高斯证明:如果费马数k为质数,那么,就可以用直尺和圆规将圆周k等分。但是,高斯本人并没有用尺规做出正十七边形,事实上,完成证明之后正十七边形的做法对数学研究者是显而易见的。第一个真正的正十七边形尺规作图法是在1825年由约翰尼斯·厄钦格(Johannes Erchinger)给出.】。
高斯(1777─1855年)德国数学家、物理学家和天文学家。高斯在童年时代就表现出非凡的数学天才。年仅三岁,就学会了算术,八岁因运用等差数列求和公式而深得老师和同学的钦佩。大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件。解决了两千年来悬而未决的难题。
1799年以代数基本定理的四个漂亮证明获博士学位。高斯的数学成就遍及各个领域,在数学许多方面的贡献都有着划时代的意义。并在天文学,大地测量学和磁学的研究中都有杰出的贡献。
作法介绍
先计算或作出cos(360°/17)
设正17边形中心角为a,则17a=360°,即16a=360°-a
故sin 16a=-sin a,而
sin 16a=2sin 8a·cos 8a=4sin 4a·cos 4a·cos 8a=16sin a·cos a·cos 2a·cos 4a·cos 8a
因sin a不等于0,两边除之有:
16cos a·cos 2a·cos 4a·cos 8a=-1
又由2cos a·cos 2a=cos a+cos 3a(三角函数积化和差公式)等
注意到cos 15a=cos 2a,cos 12a=cos 5a(诱导公式)等,有
2(cos a+co s2a+…+cos 8a)=-1
令
x=cos a+cos 2a+cos 4a+cos 8a
y=cos 3a+cos 5a+cos 6a+cos 7a 正十七边形
正十七边形
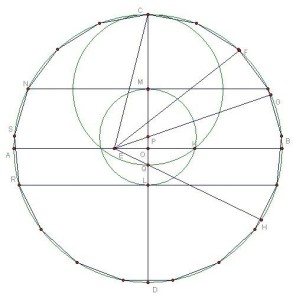 正十七边形做法
正十七边形做法
1.给一圆O,作两垂直的直径AB、CD.
2.在OA上作E点使OE=1/4AO,连结CE.
3.作∠CEB的平分线EF.
4.作∠FEB的平分线EG,交CO于P.
5.作∠GEH=45°,交CD于Q.
6.以CQ为直径作圆,交OB于K.
7.以P为圆心,PK为半径作圆,交CD于L、M.
8.分别过M、L作CD的垂线,交圆O于N、R.
9.作弧NR的中点S,以SN为半径将圆O分成17等份.
简易作法
因为360°/17≈21°10′ ,利用sinA 21°6′=0.3600可得近似角。用该方法作正十七边形总误差为17*4′=68′,在不要求十分精确的情况下还是可行的。
作法如下:
1.先画一条直线,用圆规在上面截取5条相等线段,(尽量越短越好),再截取之前四条线段的和,接续之前画的线段。这样,如果每条小线段算作0.1的话,那么整条线段就是1.8。
2.用圆规截取之前5条小线段的长,画5次,这样这条线段就是5。1.8/5=0.36。准备工作完毕!
3.另作一条直线,作垂线,1.8的线段作为对边,5的线段作为斜边,那个最小的锐角即是近似的360°/17的角。以其顶点为圆心,重复作角直至闭合。画一大圆,连接其与17条射线的交点,即可。

-
上海正艺信息科技有限公司
2025-09-28 16:30:49 查看详情


 求购
求购







