完全四点形

定义：平面上四个点(无三点共线)以及联结其中任意两点的六条直线所组成的图形称为完全四点形。

性质 ：

（1）性质1：在完全四点形的对边三点形的每一条边上有一组调和共轭点，其中两个点是对边点，另外两个点是这条边与通过第三个对边点的一对对边的交点。

（2）性质2 ：在完全四点形的的每一条边上有一组调和共轭点，其中两个点是顶点，另外一对点偶里，一个点是对边点，另外一个点是这个边与对边三点形的边的交点。

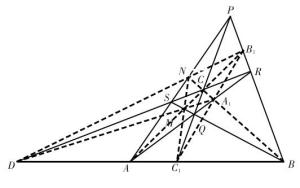图1 完全四点形的三点共线图定义：平面内无三点共线的四点及其两两连线所构成的图形，叫做完全四点形。三对对边的交点构成的三角形称为三点形。

定理：完全四点形的任意三点构成的三角形与其三点形应边的交点共线。

证明：如图1，由于S是△QRP与△ABC的对应顶点的连线的交点，设其三双对应边的交点分别为：BC与RQ的交点为A1，AC与RP的交点为B1，AB与PQ的交点为C1，则根据笛萨格定理，得到A1、B1、C1共线。

因为PQRS是完全四点形，因此可以得到以下结论：

（1）若以R为两个三角形△QPS与△ABC的对应顶点的连线的交点，设其三双对应边QP与AB的交点为C1，QS与AC的交点为M，PS与BC的交点为N，则C1、M、N三点共线。

（2）若以P为两个三角形△ABC与△SRQ的对应顶点的连线的交点，设其三双对应边AB与SR的交点为D，AC与SQ的交点为M，BC与RQ的交点为A，则D、M、A三点共线。

（3）若以Q为两个三角形△ABC与△RSP的对应顶点的连线的交点，设其三双对应边AB与RS的交点为D，AC与PR的交点为B，BC与SP的交点为N，则D、N、B三点共线。

完全四点形的调和性是高等几何的一项重要内容， 在几何学中占有重要地位。 它对初等几何的研究亦具有重要的指导意义。比如说，它在初等几何的平分角度问题、共点共线问题、中点问题、线段比值问题及平行性等问题的研究中都有广泛的应用。

调和性内容如下：

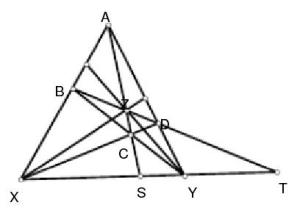图2（1）完全四点形（图2中的四点形ABCD）的两个对边点X、Y的连线交第三对对边于S、T，则(XY，ST) =-1。

（2）完全四线形 （图3中的四线形abcd）的两条对顶线x、 y的交点O与第三对对顶点相连得直线 s、t，则(xy,st) = –1。

（3）在完全四点形的对边三点形的每条边上，有一个调和点组，其中一对为对边点，另一对为该边与第三组对边的交点。

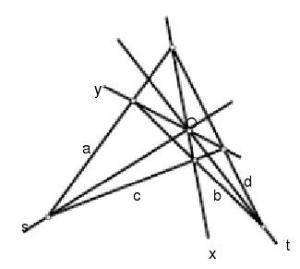图3（4）在完全四点形的每条边上有一个调和点组，其中一对为顶点，另一对中一个为对边点，一个为该边与对边三点形的边的交点。

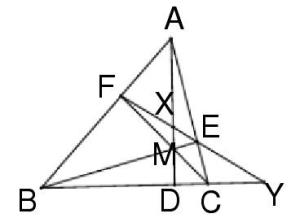图4例1：如图4， AD 垂直于 BC，M 是 AD 上的任意一点，BM 交 AC 于 E，CM交 AB 于 F，证明 ：AD 、BC 平分 DE 与 DF 所成的角。

证明：连直线 EF 分别交直线 AD、BC 于 X，Y。考察完全四点形 AFME ，由完全四点形的调和性，得 (EF, XY) = – 1, 即 D(EF, XY) = – 1 ，又因为 DX⊥DY ，所以 AD 、BC 平分∠ EDF。

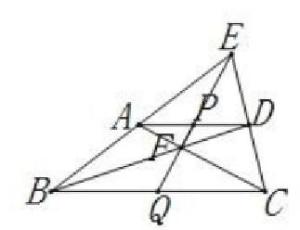图5例 2：求证梯形两腰延长线的交点与对角线的交点连线平分上下底。

证明：如图5，四边形 ABCD 为梯形，AD//BC，E、F 分别为两腰和对角线的交点。EF 交 AD，BC 于 P、Q。考察完全四点形 EAFD。设 AD ×BC=G∞。由完全四点形的调和性知 (BC, QG∞) = –1，因为 AD//BC，故 G∞是无穷远点，从而 Q为 BC 的中点。

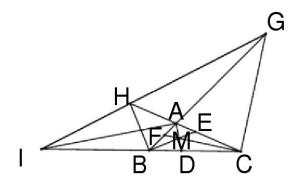图6例 3：求证三角形的三条外角平分线和对边相交所得三点共线。

证明：如图6所示， ABC 的三条外角平分线与对边交与G，H，I。设 ABC 的三条内角平分线交与点M。 AD、BE、CF 交与点 M，则有迪沙格定理知，两个三角形对应边连线的交点共线。 设 AB 与DE 交与 G’，AC 与 DF 交与 H’，BC 与 EF 交与 I’，则 G’、H’、I’三点共线。又 ACB 的外角平分线交AB 与 G，ABC 的外角平分线交 AC 与 H， CAB 的外角平分线交 BC 与 I，所以有（BA,FG）=-1,(BC,DI)=-1,(CA,EH)=-1. 在完全四点形 CDME 中由调和性知（BA， FG’）=-1。所以有（ BA,FG）=（BA ，FG’）=-1.，即 G 与 G’重合。同理可知， H 与 H’，I 与 I’重合，所以 G，H，I 三点共线。

例 4：用无刻度直尺完成以下作图：已知一线段 BC 中点 Q 及其线外一点 A，求过 A 作该线段的平行线。

方法：

（1）连接 BA ，并在其延长线上取一点 E。

（2）连接 CA ， QE 交与点 F。

（3）连接 BF、CE 交与点 D。

（4）连接 AD ，则直线 AD 为所求直线。