- Jaccard系数

Jaccard系数
系数基本概念
定义
给定两个集合A,B,Jaccard 系数定义为A与B交集的大小与A与B并集的大小的比值,定义如下:
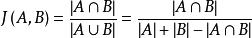
当集合A,B都为空时,J(A,B)定义为1。
与Jaccard 系数相关的指标叫做Jaccard 距离,用于描述集合之间的不相似度。Jaccard 距离越大,样本相似度越低。公式定义如下:
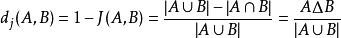
其中对参差(symmetric difference)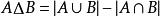 。
。
性质
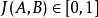
相似性
非对称二元属性的相似性
在数据挖掘领域,常常需要比较两个具有布尔值属性的对象之间的距离,Jaccard距离就是常用的一种方法。给定两个比较对象A,B。A, B 均有n个二元属性,即每个属性取值为{0,1}。定义如下4个统计量:
![]() :A,B属性值同时为0的属性个数;
:A,B属性值同时为0的属性个数;
![]() :A属性值为0且B属性值为1的属性个数;
:A属性值为0且B属性值为1的属性个数;
![]() :A属性值为1且B属性值为0的属性个数;
:A属性值为1且B属性值为0的属性个数;
![]() :A,B属性值同时为1的属性个数;
:A,B属性值同时为1的属性个数;
如下图数示:

显然有
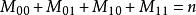
Jaccard 系数:
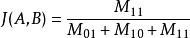
Jaccard距离:
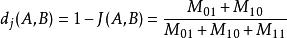
广义系数
广义Jaccard系数
(1)给定两个n维向量 则 Jaccard 系数定义如下:
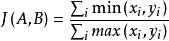
(2)给定两个关于 的非负函数f和g,则 Jaccard 系数定义如下:
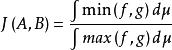
主要应用场景
比较文本相似度,用于文本查重与去重;
计算对象间距离,用于数据聚类等。
应用举例
项目相似性度量是协同过滤系统的核心。 相关研究中,基于物品协同过滤系统的相似性度量方法普遍使用余弦相似性。 然而,在许多实际应用中,评价数据稀疏度过高,物品之间通过余弦相似度计算会产生误导性结果。 将杰卡德相似性度量应用到基于物品的协同过滤系统中,并建立起相应的评价分析方法。 与传统相似性度量方法相比,杰卡德方法完善了余弦相似性只考虑用户评分而忽略了其他信息量的弊端,特别适合于应用到稀疏度过高的数据[2]。

-
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-10-06 12:04:01 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-10-06 12:04:01 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-10-06 12:04:01 查看详情 -
长安凯程GDI双侠成都上市 或将于下半年上市
2025-10-06 12:04:01 查看详情 -
西安大众速腾现金优惠2.3万 成都沃尔沃XC90优惠三万元
2025-10-06 12:04:01 查看详情 -
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-10-06 12:04:01 查看详情 -
长安凯程GDI双侠成都上市 V70/V100等车上市
2025-10-06 12:04:01 查看详情 -
将于上海车展上市 Ocean曝光
2025-10-06 12:04:01 查看详情 -
保时捷Taycan国内上市 55周年纪念版上市
2025-10-06 12:04:01 查看详情 -
哈尔滨沃尔沃XC40优惠达4.7万 优惠7万元
2025-10-06 12:04:01 查看详情


 求购
求购

