双线性模型

称随机序列服从双线性模型，如果

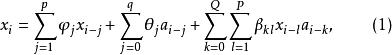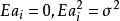其中为随机序列，。当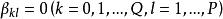，则(1)式成为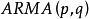模型，因此双线性模型是线性模型的直接推广。

双线性模型最早来自经济学上的问题。在经济领域有着广阔的背景。极大似然估计和矩估计都可用以估计双线性模型参数，但从现有的研究成果来看，统计推断的结论还不甚完备^[2]。

双线性模型是线性模型的直接推广，使用双线性模来描述某些非线性现象要比用线性模型更精确。由于目前尚无辨识一般双线性模型的强有力的准则和建模方法，其应用只限于几种简单的模型。

在一般的双线性模型(1)中，

(1) 若q<0，则(1)式变为

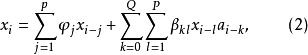我们称(2)式为关于齐次的。

(2) 若不全为零，则(1)中的系数为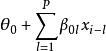，此时预报误差的大小依赖于过去的值，这种误差称为异样误差，我们称这种模型为异样的。

(3)若全为零，则(1)式变为

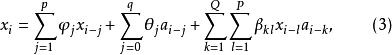我们称(3)式为非异样的。

(4)若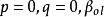全为零，则(1)式变为

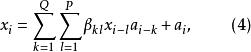我们称(4)式为全双线性的。

若在全双线性模型(4)中，记

则(4)式可写为

(5) 在(5)式中，若当时，，即B的主对角线左下方的元素全为零，则称(5)式是右上角模型；若当时，，则称(5)式为左下角模型；若当时，，则称(5)式为对角线模型。‘

设当时，与独立，在这种条件下，右上角模型

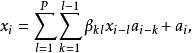中每一双线性项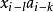都是两个独立随机变量的乘积。而左下角模型和对角线模型均不具备这一性质^[2]。