- 应力空间

应力空间
概念
主应力空间和π平面
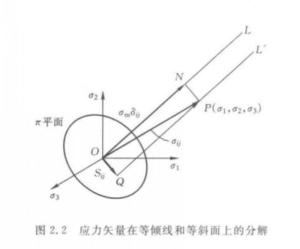 图1一点应力状态的表示可采用六个独立的应力分量.也可以用三个主应力的大小及其相应的三个主方向,还可以用应力张量的三个不变量及应力主方向。如同在三维空间内x,y,z的三个坐标值可确定空间一个点的位置一样,确定一点应力状态的六个独立应力分量也可在虚构的六维应力空间中表示。所谓六维应力空间,就是以六个应力分量为六个坐标轴的假想空间,该应力空间中的任一点都表示一个应力状态。考虑到材料是初始各向同性的,从建立屈服条件的目标出发,只要知道三个主应力的大小即可。于是,如将三个主应力σ1,σ2,σ3取为三个相互垂直的直角坐标轴而构成一个空间直角坐标系(见图1),则该空间中的一点P就对应于物体中某点的应力状态(σ1,σ2,σ3),或者用矢量
图1一点应力状态的表示可采用六个独立的应力分量.也可以用三个主应力的大小及其相应的三个主方向,还可以用应力张量的三个不变量及应力主方向。如同在三维空间内x,y,z的三个坐标值可确定空间一个点的位置一样,确定一点应力状态的六个独立应力分量也可在虚构的六维应力空间中表示。所谓六维应力空间,就是以六个应力分量为六个坐标轴的假想空间,该应力空间中的任一点都表示一个应力状态。考虑到材料是初始各向同性的,从建立屈服条件的目标出发,只要知道三个主应力的大小即可。于是,如将三个主应力σ1,σ2,σ3取为三个相互垂直的直角坐标轴而构成一个空间直角坐标系(见图1),则该空间中的一点P就对应于物体中某点的应力状态(σ1,σ2,σ3),或者用矢量![]() 表示该点的应力状态,称为应力状态矢。这个空间就称为主应力空间,它是由Haigh-Westergaard提出的。在载荷改变的过程中,物体内各点的应力状态在不断地变化,在应力空间中相应的应力点也在不断地改变其位置.则这些应力状态矢的矢端描出的轨迹就称为相应点的应力路径(历史),即应力空问中的一曲线表示了一点应力状态的变化过程。
表示该点的应力状态,称为应力状态矢。这个空间就称为主应力空间,它是由Haigh-Westergaard提出的。在载荷改变的过程中,物体内各点的应力状态在不断地变化,在应力空间中相应的应力点也在不断地改变其位置.则这些应力状态矢的矢端描出的轨迹就称为相应点的应力路径(历史),即应力空问中的一曲线表示了一点应力状态的变化过程。
性质
应力空间中线与面的性质
设以i,j,k表示主应力空间中三个坐标轴的单位向量。今在应力空间中做一直线L,它过原点O,且与三个坐标轴的夹角相等,称之为等倾线L(也有称等斜线)。由于L上任一点在三个坐标轴上的坐标是相等的,所以L直线的方程是
![]()
也就是说,L线上各点代表均匀应力状态,其应力偏量为零。再在应力空间中观察过原点且与L垂直的平面.其方程式为
![]()
由于在这个平面上所有各点的平均应力为零,只有应力偏量,因此,将其称为偏量平面π。位于π平面上的点时与应力偏量相对应的。
现对矢量![]() 做如下分解
做如下分解
![]()
式中:![]() 为应力偏量;
为应力偏量;![]() 为静水应力。因
为静水应力。因![]() 在三个坐标轴上的投影相等,故必与等倾线L重合。又由
在三个坐标轴上的投影相等,故必与等倾线L重合。又由
![]()
知![]() 必在π平面内。
必在π平面内。
注意,过π平面上任意一点且与π平面相垂直做一直线L',该线上各点的应力偏量是相同的。因静水应力对材料的塑性特性没有影响,故考察塑性变形与应力状态之间的关系时,可以着眼于π平面,只考虑在该平面的投影(如![]() )即可,因为应力空间中任一点所代表的应力状态的偏量部分必落在π平面上。
)即可,因为应力空间中任一点所代表的应力状态的偏量部分必落在π平面上。
相关性研究
三种六面体约束应力空间的相关性研究
弱平衡、正交性和能量协调条件是构造高性能杂交元的三种手段,三个条件同时满足是一种理想的应力设计方案,四边形单元CH(0-1)的应力是这种理想方案的一个代表。该研究在剖析出三线性等参变换中众多参数的几何意义之后,研究了六面体情况下约束线性应力关于Wilson位移满足三种不同条件的应力设计方案,结论是对于一般网格,能量协调与正交性条件约束下的应力空间不一定相同,弱平衡条件不一定自然满足;只有当网格满足一定的条件时,这两种应力空间才相同;当采用折半剖分方案时,这两种约束下的应力模式相差高阶无穷小。数值试验结果也肯定了以上结论。

-
实拍江铃新宝典(图文) 空间满足家用
2025-10-23 09:44:43 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-10-23 09:44:43 查看详情 -
江铃福特轻客持续打造最优TCO 空间满足家用
2025-10-23 09:44:43 查看详情 -
航天恒星空间技术应用有限公司
2025-10-23 09:44:43 查看详情 -
上海车展实拍江铃福特领裕 空间满足家用
2025-10-23 09:44:43 查看详情


 求购
求购




