测不准关系

　　测不准关系即不确定性原理.

　　一个微观粒子的某些成对的物理量不可能同时具有确定的数值，例如位置与动量、力一位角与角动量，其中一个量越确定，另一个量就越不确定。它来源于物质的二象性.测不准关系是从粒子的波动性中引出来的。

 粒子的波动性-内部结构模型图　　测不准关系有两种形式，一种是动量-坐标的关系，另一种是能量-时间的关系。  粒子的波动性-内部结构模型图

　　若位置的不确定度为Δx，动量的不确定度为Δpx，则Heisenberg测不准关系表示为

　　Δx Δpx ≥ ħ 或者 Δx Δkx ≥ 1

　　测不准关系即表示Δx与Δpx，或者Δx与Δkx的乘积不能为0。

　　对于y和z方向上的测不准关系，分别有：

　　Δy Δpy ≥ ħ 或者 Δy Δky ≥ 1

　　Δz Δpz ≥ ħ 或者 Δz Δkz ≥ 1

　　值得注意，坐标和动量不能同时确定，是指同一个方向上的坐标和动量，而对于不同方向上的坐标和动量则测不准关系不成立，即可以精确地确定。例如，Δy与Δpx可以同时确定，即它们的乘积可以等于0。

　　例如自由粒子，其势能V=0，波函数是行波形式的平面波。这表明自由粒子在空间中各处出现的几率为常数，即位置不确定（亦即位置的不确定度Δx=∞）；而自由粒子具有一定的波矢k和对应的de Broglie波长l，则具有确定的动量（p=ħk=h/l），即动量的不确定度Δp=0。这符合测不准关系的限制。

　　因为微观粒子的总波函数包含有两个部分：一个与坐标有关，另一个与时间有关。其中与坐标有关的部分，引起了(1-24)式的测不准关系；而与时间有关的部分，也将引起类似的测不准关系，这就是能量E（E=ħω）和时间t的测不准关系：

　　ΔE Δt ≥ ħ 或者 Δω Δt ≥ 1

　　这就是说，微观粒子的能量E（或者角频率w）和微观粒子具有该能量的持续时间Δt（或者测量该能量的时间），不能同时确定。

　　实际上可以证明，任何两个不对易的力学量算符之间都满足类似的测不准关系（即不能同时确定）。

　　测不准关系反映了微观粒子的波动性，可以用来解决许多有关的问题。

统计量子力学与经典量子力学间存在深刻的理论断层，它使得理论与实验观测不能在理论中自封闭，这是量子论的基础性困难。坚信“偶然的背后仍是偶然”的科学很难称其为“科学”（至少能使它的预示性光芒变得暗淡）。所以在肯定统计的同时，有必要作必然性探究和追踪。在量子力学诞生之初的二、三十年时间里，人们都强烈地希望找到一种从经典力学到量子力学的过渡理论（即希

望到量子力学与经典力学相容的结果）。只是抱

这种希望的那辈人在长期的等待中总是失望，且大部分都带着失望回归自然了。权威的新一代人和仍然留守人间的老一辈人现在再也没有那种强烈的希望了（或者只是强制压抑着这种希望）。可是，本文有充足的理由重新点燃这种希望之火。

量子力学大厦是建立在否认轨道运动、排斥经典运动规律的基础上的，而否认轨道运动的依据是Heisenberg 导出的测不准关系及其非决定论意义。论证了测不准关系不能否认轨道运动规律，对量子力学的影响是可想而知的。敬请读者不要轻易用非逻辑因素否认此时产生的“第一感觉”。不然的话，就很容易被习惯性思维所左右。

有人说过“美的东西都是简单的东西”。作者相信简洁就是一种美，或美的东西都有简单的一面。尽管本章所使用的逻辑方法是比较简单的，但是，只要文中的逻辑推衍过程是严格的，人们改变观念的犹豫反而会更小。在科技史中，不乏“用简洁的方法说明深刻的问题”的例证。另外，“简洁”向来都是经典力学的特点之一，只要利用了经典力学，简洁的一面就是不可避免的。

1.1 由经典运动定律变形得到测不准关系的几种方式[2]

根据带电粒子绕中心电荷作匀速圆周运动方程可以得到“p·r只与相互作用的电量和速度有关而与运动物体的质量无关”的结论。根据曲率都与曲率半径成反比的规律可以得到“非决定论意义测不准关系只是决定论意义确定度关系在随机干扰不可忽略时，取f(q, υ)≈1的特例”。动量与位置（或能量与时间）测量精确性的Copenhagen极限被打破。

1.1.1 利用经典的光线偏折公式导出测不准关系（不确定度关系）

最初的爱因斯坦光线偏折公式是根据牛顿引力理论推导出的，属于经典力学运动公式的范畴：

(1)

若速度不是 c 而是一般速度υ，且高速粒子在掠过裸核时的线速度变化可以忽略不计，υ被认为是常数, 则（1）式变为 φg=2GM/υ2 r. 由于牛顿力和库仑力都是保守力，且极为对称, 因此, 对于电子注掠过质子表面而言, 库仑力导致的偏转角 φe 与牛顿力导致的偏转角φg 之比等于这两种力的强度之比：φe /φg=(K/G)Qq/Mm. 将 φg=2GM/υ2r 代入该比例式， 可得 φe = Qq /2πε0 mrυ2 考虑到 Q = Ze, q = e，有

φe = Z e2/2πε0 r mυ2. (2)

将 υ 当作常数，将GMm/R2换为KQq/R2依照爱因斯坦求积分的方法，求可直接得到与（2）式类似的φe = e2/ r mυ2. 将 p=mυ、ћ =h/2π、α=e2 /2ε0 hc 代入（2）式, 可得

φe= (2Zαc /prυ)ћ, r=2Zαc ћ /mυ2φe. (3)

当 φe 特别小时有 sinφe =φe 的关系。将 sinφe =φe代入（3）式，并令 psinφe =Δpx，可得

r·Δpx = (2Zαc/υ) ћ. (4)

（3）式（4）和式都是电子射线在电场中偏转的计算公式。

若电子射线穿过的是由两个平行布喇格（Bragg）平面构成的单缝，缝的两侧的有效核电荷数都对入射电子产生影响。因此，当我们只考虑单侧偏转时，r 最大不超过缝的宽度 △x, 即 r≤Δx，（4）式变为

Δx·Δpx≥(2Zαc/υ) ћ. (5)

当υ≤2Zαc 时, (5) 式变为

Δx·Δpx≥ћ. (6)

在一般情况下（6）式和υ≥2Zαc时的Δx·Δpx≤ћ可以合并为

Δx·Δpx= f(q，υ)ћ. (7)

1.1.2 从电子受库仑力作用的情况出发导出测不准关系

一个电子在“匀强电场”空间中所受到的力等于 e2 / r2，即F＝e2/ r2, 其中 r 是电子与缝壁之间的垂直距离。根据基本运动定律知 F＝ma，s＝(1/2)at2. 或中 m 为电子的质量，s 为电子自由下落的距离。设缝深为L，则电子穿过它所花的时间为t＝L/υ秒。这样，我们可得到

s＝e2L2/ mυ2 r2. (8)

如果电子射线的偏转角为φ，而且很小，就有sinφ＝s/L和

sinφ＝ e2L/mυ2 r2，，敬 . (9)

（9）式就是当一个电子掠过一个长度为 L 的“匀强电场”空间时，r、υ、φ三者之间的关系。如果一束电子射线像一束光子掠过太阳表面那样掠过一个重核的表面，考虑电子射线在 L=2r 的范围内发生偏折，就有

r·sinφ＝2e2/mυ2. (10)

若电子穿过的是整齐排列的核组成的一条缝，那么，电子与缝壁之间的相互作用距离不会超过缝宽Δx) (即 r≤Δx).于是 sinφ≥. 令 p＝mυ、p·sinφ＝Δpx，我们有

Δx·Δpx≥2e2/υ. (11)

考虑到精细结构常数α＝e2/2ε0hc，当时，可得

Δx·Δpx≥h. (12)

(4) 式（9）式和 (10) 式的导出过程都表明: 只要没有发生随机的干扰，瞬时的 r 可以是一个瞬时的曲率半径，Δpx就与某个时间间隔之内的瞬时曲率的积分相对应，足够大也不表示动量测不准；当我们给予运动的微粒一个其量为 Δx 的随机空间限制, 就会产生一个大小为 Δpx 的动量不确定度, (6) 式和 (12) 式不总是表示不确定度关系。当测不准关系表示线动量与曲率半径之积与普朗克常数之间的函数关系时，在没有随机干扰时（或不测量时），粒子就被允许是定域的和有轨道的。

曲率都与曲率半径成反比是一条数学定律。它的表达式为：r·K=1。两边同乘以p并变形，得：r·p=p/K.。对于一小段弯曲而言，K=α/Δs，当α很小时，有sinα ≈ α 的关系，令p·sinα＝就有：r·Δpx = p·Δs = mυ·Δs. 由于mυ·Δs与普朗克常数的量纲相同，在微观粒子衍射实验中，∆s与缝深相当且相对不变，而粒子的线动量或线速度相对不变。因此，r·Δpx = mυ·Δs可写为r·Δpx µ ћ” 或

r·Δpx= f(q，υ)ћ，（13）

此处，f(q, υ) 是一个与质量和速度大小有关的无量纲系数。只要排除了随机干扰，（13）式的决定意义就是广泛适用的。

质量不同的运动物体，其f(q, υ)的大小不同。由于我们不可能在一次讨论的过程中更换入射粒子从而改变f(q, υ)的大小，因此（13）式表达的意义与 “Heisenberg 不确定度关系” ΔpxΔx ≥ћ表达的意义在ΔpxΔx的值大于和等于ћ的范围内是相同的。（13）式显然比ΔpxΔx≥ћ 更精确（适用范围更广）。正是由于ΔpxΔx≥ћ关系的不精确， 才使人们常常错误地认为ΔpxΔx = ћ [即以f(q，υ)≈1的特例片面地代替f(q, υ)的广泛的取值范围]，从而得出了ΔpxΔx ≥ћ的式子对宏观物体没有意义的错误结论。只有严格地证明了f(q，υ)的值只能在“从等于1到比1 大得不多”的范围内，且存在随机干扰，Copenhagen学派建立的量子力学解释系统才是有效的。否则，Copenhagen 诠释就有强权性和欺骗性。 如果ΔpxΔx的取值只有下限ћ而没有上限（Heisenberg测不准关系就是这样表示的。如果你认为有上限，需要严格证明上限是多少），就可以在 [1，∞] 区间内取值，若取ΔpxΔx =1035 ћ，这时就可利用测不准关系有意义地讨论重达1公斤的入射物体了。标明了ΔpxΔx≥ћ但只取ΔpxΔx= ћ这个特例，显然是极其片面的。

在电子衍射实验之中，有许多入射粒子偏折到了衍射环之外很远的地方，实际上是用实验方法证明了Δpx与Δx之积可以比ћ大许多倍（偏折很小则是表明Δpx与Δx之积可以比ћ小许多倍），也证明了仅仅选择ΔpxΔx= ћ不符合实验事实。用落点的概率分布解释也是不科学的。因为，在微观体系中，随机干扰程度不会与实物粒子衍射实验中的相同，原子、分子中的电子有序排列表明完全可以用未受到随机干扰来解释。粒子在云室中受到的干扰也与在狭缝中大不一样（因为大云室中微粒不会发生衍射）。一旦没有随机干扰，就应该采用（7）式或（13）式或（15）式描述。存在动量与线度之积不受运动物体的质量限制的情况。

电子在中心电荷为 Ze 的力场中的运动方程为Ze2/(4πε0r2)= mυ2/r。将mυ2=2E = pυ代入此式，可得

Er = Ze2/8πε0=1.15356Z×10-28J·m

= (1.09385Z×106 ћ)m·s-1；（14）

pr = Ze2/4πε0 υ

=[(1.09385 ×106 ћ)(2Z /υ)m·s-1

=(Zc/υ) × 7.29738 ×10-3 ћ.

令f(q, υ)= (Zc/υ) × 7.29738 ×10-3，就有

pr = f(q，υ)ћ （15）

动量与线度之积与普朗克常数比较正是测不准关系的一种形式。（15）式中的动量与线度之积与速度有关而与质量无关，因此（15）式对于宏观物体（例如灯草球绕中心电荷运动）和微观物体（如一个原子）都适用，且是相互垂直的，不受二者必须同向的限制。类似地，对于地球绕太阳的运动，我们有GMm/r2= mυ2/r和Er = GMm/2及pr = GMm/υ的关系。可见，“对于既定的束缚态匀速圆周运动动，能量与线度之积、动量与线度之积都是一个确定的值的规律”是普适的，当Zc/υ等于103（即υ 在10-2Zc到10-3Zc之间）时，（15）式变为p·r≈ћ。例如，原子分子的电子的速度约为Zαc（α 是精细结构常数，大小为1/137），电子运动的p·r正好与普朗克常数相当（如果υ≤Zαc，则p·r ≥ћ）。

将pυ=2E 代入r∙p∙sinθ = f(q，υ)ћ，考虑到匀速曲线运动有的关系，我们有。根据曲率的定义可知，对于匀速曲线运动，，而r·K=1。于是变为

EΔt = f(q, υ)ћ。（16）

（16）式是（13）式的另一种表现形式。（13）式是曲率与曲率半径成反比的反映（在此表示：对于一个既定的入射粒子，曲率半径与偏转角θ 或弯曲程度sinθ 成反比），而（14）式、（15）式和（16）式则是经典运动定律的变形式。故，我们可以肯定上述推导过程和得到的结论是可靠的，还有利于揭示测不准关系的本义。

2测不准关系的本质和适用范围浅析

虽然以上相关式子中的f(q, υ)都是一个函数，但是，它们都是无量纲的。由（3）式还可以看出，当Z随机地改变时，pr= f(q, υ)ћ中的p和r就至少有一个是不确定的（即是一个随机变化的范围）。所以，我们肯定：ΔpxΔx = f(q, υ)ћ包含ΔpxΔx≥ћ，决定论意义的测不准关系是存在的，Heisenberg 测不准关系及其非决定论意义是决定论意义的测不准关系“在随机干扰存在的前提下，f(q，υ)≈1时的特例”。

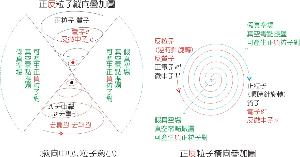
由于（6）式和（12）式都是由 F＝ke2/ r2, F＝ma, s＝(1/2)at2 等经典运动定律得到的，因此，（6）式和 (12) 式不能否定轨道运动，它们可以表示曲率与曲率半径之积等于一个常数。就上述推导过程而言，（8）式和（9）式仍然没有甩掉“表示曲率与曲率半径成反比”的意义，不宜冠以“不确定度关系”的名称，即使认为它们表示“不确定度关系”，那也是给予了粒子束流一个空间限制或提供了一个受到随机干扰的机会（例如：制造一个隘口式关卡或提供一个干涉不可预测的环境）造成的。就是说，测不准关系至少可同时表示“曲率与曲率半径成反比”和“不确定度关系”两种意义。我们再也不能武断地认为（6）式和（12）式仅具有 Heisenberg 意义了（测不准关系的Heisenberg 意义等同于测不准关系的非决定论意义）。只要利用 r≤Δx 的关系将（6）式和（12）式中的 Δx 换为 r, 就可以利用（6）式和（12）式的上源准确计算单个粒子穿过狭缝时的偏转角。这一功能是 Heisenberg 意义的同形关系式所没有的。既然测不准关系具有决定论和非决定论的双重意义这使我们不便于继续将Heisenberg导出的测不准关系叫做“测不准关系”，最好把形式类似的关系式都叫做Heisenberg 关系，并用“单一统计意义”、“双重意义”、“非统计意义”和“纯决定论意义”等定语区分它们的子类。从本自然段开始都这样处理。所以，我们得到了这样的结论：Copenhagen 学派实际使用的单一统计意义Heisenberg 关系是双重意义Heisenberg关系“在随机干扰不可忽略的前提下，f(q, υ)≈1时”的特例；或者说，单一统计意义Heisenberg 关系是纯决定论意义Heisenberg 关系的一个近似。可用图形表示这一结论：

就是说，在一定重要条件下，决定论意义的Heisenberg关系与单一统计意义的Heisenberg关系可以相互转换。根据这个结论可以预言：凡是相互干扰可以忽略的场合，测不准原理都不适用。在做引力相互作用实验时，随机干扰都可以忽略不计。所以，引力实验不能测出量子化的效应，在实用意义上，引力不可量子化。

为什么中性粒子射过狭缝也会发生衍射且符合关系呢？一种解释是“粒子具有波-粒二象性”。对于两个平行布喇格（Bragg）平面构成的单缝，其中的空间不是完全空旷的空间，而是充满电子的空间，中性粒子穿过这类有一定障碍的狭窄空间一定会出现随机分布的状态。这样，凡是位置由sinθ＝(λ/Δx) 决定的中性粒子流，只要它们具有足够的波动性，且两粒子的光程差为半个波长的整数倍，就会发生干涉，狭缝宽度 Δx 是不变的，入射速度不变时波长λ就不变，所以由 sinθ＝(λ/Δx) 决定的暗纹的位置就是很有规则的，衍射图样也就能形成。将sinθ= (λ/Δx)代入 Δpx ＝p sinθ 可得 Δpx＝p(λ/Δx)，再将 p＝(h/λ) 代入上式，可得

ΔpxΔx＝h. （17）

(17) 式的推导过程表明：形如 ΔpxΔx＝h 的关系的决定因素之一是随机干扰，之二是粒子的波-粒二象性。本文介绍Heisenberg关系的推导过程并不强硬地支持电子的衍射图形是由点电子直接造成的（因为， 如果没有波动性，受到随机干扰的微观粒子就只能形成界限模糊的亮斑而不能形成清晰的条纹）。可见，当粒子（无论是中性的还是非中性的，只要波动性表现突出）在穿过有一定障碍的狭缝时，都会产生衍射图样，统计结果符合不确定度关系。中性粒子的衍射实验结果可用形如 (17) 式的单一统计意义解释。（6）式、（12）式和（17）式都可用于讨论多个粒子穿过狭缝时的统计结果。

如果高速粒子穿过狭缝时发生衍射的原因是“粒光效应”——一种与“光电效应”的逆过程类似的效应，则会对“波-粒二象性”的适用范围产生巨大的影响。需要做进一步的实验以检验粒子衍射效应的起因到底是“因随干扰而测不准的本性”还是“粒子的波-粒二象性”还是“粒光效应”还是三者兼而有之。这三种情况造成的衍射都可以用双重意义Heisenberg 关系描述，双重意义Heisenberg 关系的上源公式之一可以用于描述经典的粒子运动（如云室中带电粒子径迹的偏转角就可以用（9）式或（10）式计算）。详情除了下一自然段即将介绍外，在3.1.2节还要作一些补充。

（6）式和（12）式是轨道运动方程的无歧义的变形式。它表示不测量时(或作无随机干扰的测量时)位置和动量可同时具有确定的值。(13) 式的非决定论意义表示，一旦受到随机干扰，位置和动量就不能同时测准，并不能强硬地表示：即使不测量，微观粒子也不能同时具有准确的位置和动量。既然根据射线的波动性、经典力学运动规律和受到随机干扰后的统计规律都可以得到形如 Δx·Δp～h 的式子，那么，Heisenberg 关系就既是 ① 波-粒二象性（或粒光效应）的反映又是 ② 轨道运动规律的反映也可以是 ③ 因随机干扰而测不准的反映。在逻辑上我们不能排除量子力学体系中存在与“不测量”和“无随机干扰地测量”的对应状态（目前认为“无”主要是因为找不到这种状态。第4章给出了有这种功能的电子结构模型），因此，在任何情况下都千篇一律地取意义 ③ 是片面的。我们应该将“测不准原理与经典规律相互排斥”的旧观念改变为“Heisenberg 关系与经典运动规律相容”的新观念。意义 ② 和 ③ 同时存在表明Heisenberg 关系并不能成为否认轨道运动的充足理由。并可预言：凡是有可观随机干扰的测量结果或受试对象的波动性比较突出的测量结果必然符合统计解释；允许随机干扰消除得可以忽略的测量结果符合定域实在论的解释；受试对象的波动性突出或随机干扰消除得不彻底但相对较弱的实验结果可同时采用统计解释和定域实在论的解释。

3 Heisenberg关系具有的决定论意义的发现对量子力学测量观的影响

得到Heisenberg 关系的决定论意义的逻辑过程对正统量子力学观念多少有一些影响。下面作一些简单地介绍，意在供大家参考的同时聊表Heisenberg 关系的决定论意义这项发现的部分意义。

实际上，由于动量与线度之积的量纲与普朗克常数的量纲相同，因此对于任何体系中的线度与动量之积都与普朗克常数只差一个无量纲的倍数。这种情况反映了形如Heisenberg关系的式子的适用范围是很宽广的。谁认本文导出的具有决定论意义的Heisenberg关系在微观体系中不适用，谁举证。 “单一统计意义Heisenberg关系在宏观体系中不适用”与“决定论Heisenberg关系在微观体系中不适用”两种认识的理由的可靠程度相等。即使在微观体系中干扰不可消除，也不能因此而认为f(q, υ)必须约等于1。如果测不准关系表示动量与曲率半径之积与普朗克常数之间的函数关系，在没有随机干扰时（或不测量时），粒子就被允许是定域的，同样被允许是有轨道的。

3.1 对一些量子力学观念的影响

3.1.1 影响“原子分子中的受约束电子只能与穿过狭缝时的电子对应”的观念

人们还把这种观念推广为“只要处于被测状态的微观粒子就处于被随机干扰的状态”。但是，即使没有用经典方法导出（5）式和（11）式，比较起来，原子分子中的受束约电子所处的状态，更接近于电子在微观尺度范围内掠过核表面受到有规律的影响时所处的状态，而偏离电子穿过一条狭缝受到随机干扰的状态。认为微观世界中粒子的所有作用都形成随机干扰显然过于武断了。原子、分子中的电子的环境虽然有些错综复杂，但是，它们的运动是有序的（无论是复杂的原子还是最简单的氢原子，跃迁时的发射光谱、测得的轨道磁矩、轨道角动量和电子分布的理论都证明了原子中的电子运动是“有序”的（没有充足的理由强硬地认为“只有统计之后才是有规律的”），我们不能肯定氢原子中的电子受到了核的随机干扰）。只要“有序”就有“能被精确预测”的可能，有序正是有明确规律的反映。如果是“只有在统计之后才显示出规律”就不是“有序”。一句话，我们没有充足的理由认为原子、分子中的电子所受到的干扰一定是“随机干扰”而不是“有规律地干扰”。在“Heisenberg关系的决定论意义”发现之后可坚定这一信念。

3.1.2 影响“Heisenberg 关系与经典运动定律不相容，在微观世界不能使用轨道概念”的观念

Heisenberg 关系的非统计意义的存在，决定了在原子分子中，只有先否定了轨道运动，才能肯定“测不准”，绝对不是先有测不准原理后有“对轨道运动的否定”。换言之，我们不能凭借“测不准原理”而否定轨道运动。

既然 (6) 式和 (12) 式都是轨道式力学运动规律的特殊表现形式, 就表明: 空间坐标和动量之积正比于普朗克（Plank）常数也可以是因果关系的反映。(6) 式和（12）式都是当入射速度一定时，入射位置 r 和偏转角φ 之间的因果关系，而不始终是两个不确定度范围（Δpx 和 Δx）之间的关系（即不始终是不确定度关系）。当入射粒子受到了随机干扰时，(6) 式和（12）式中r 和φ 之间的因果关系就被无法精确预测地破坏了，(6) 式和（12）式就成了两个不确定度范围（Δpx 和 Δx）之间的关系（即名副其实的不确定度关系），可用于计算统计结果（这一点也已被多数教科书证明了）。所以，形如（12）式的关系至少具有决定论和非决定论的双重意义，定域实在论解释与统计解释相容有了理论依据。谁都知道，我们不能因为射门足球的落点和经过的路径符合统计规律而否认足球能作轨道运动。像这种情况一样，我们也不能因为受到了随机干扰的粒子符合统计规律而否认它们未受到随机干扰（或受到确定的干扰）时有确定的运动轨道。在量子力学计算中，统计规律与势能函数（V =e2/r）同时使用，支持“点粒子概念和经典运动规律仍然有效”的信念，需要“Heisenberg关系与经典运动定律相容”的观念。在微观世界中，是利用Heisenberg关系的统计意义？还是使用它的决定论意义？完全取决于随机干扰是否可以忽略。

新的对应观念是，若能确认量子体系中微粒的运动没有受到随机干扰，就可以使用经典轨道概念。

3.1.3 影响“只能直接测量不可间接测量”的观念（即影响“触摸式测量观”或极端实证哲学）

持这种测量观的人认为即使知道粒子和起点和终点也不能推测出粒子从起点到终点的路径。观察云室中一次高能 -量子的衰变过程，知道了光子的出发点和衰变点，按常理再根据光子的速度和走过的距离就可以推测出光子走过的路线。但正统量子学者不承认这个光子在起点与终点之间的各个时刻的位置和动量同时间接地被测准了。更详细的说明请参阅3.2.1节《云室中带电粒子径迹的意义》。

“触摸式测量观”是指直接触摸到（或探测到）了才认为是测到了，没有直接触摸到（或探测到）就认为是没有测到。它是核心是，只承认直接测量结果而不承认间接测量结果。这种测量观的是“在微观世界中不能使用轨道概念的观念”将实证哲学推向极端而产生的，而不能使用轨道概念的观念又来源于单一统计意义Heisenberg 关系。①单一统计意义Heisenberg关系、②不能使用轨道概念、③触摸式测量观三者之间形成了一种恶性循环：②依靠①，③依靠由②，而①需要②和③来维护、支持甚至印证。变更了①就动摇了②和③立足的基石。

新的对应观念是，在微观世界中我们也可以像探测夸克一样作间接测量和常规逻辑推衍。

3.1.4 影响“所有微观粒子在微观尺度下都不能同时测准位置和动量”的观念、实验设计和实验现象解释

在Heisenberg关系的决定论意义存在的前提下，尽管 Δpx 是一个可观的数（曲率是一个不小的值），但只要是一个定数，也认为动量被测准了。就像测准了回旋加速器中的粒子的动量（或地球公转时的动量）的情况一样。我们在本文导出的Heisenberg关系中并不总是表示只有统计意义的不确定度的前提下下讨论“测不准原理”。

（8）式的推导过程可知，尽管 Δx 是狭缝宽度，在一定条件下可以表示位置不确定度，但能表示单次测量时一个带电粒子在掠过裸核（或带电平行板）时的准确位置的不是 Δx而是粒子距力源中心的距离r. （9）式和（10）式成立表明，测准带电粒子的入射位置至少有两种方式（一种是制造 Δx→0 的缝让其受到不可预测的干扰，另一种是让它掠过一块有规律的电场空间）。 容易看出，其中的最佳方式肯定不是让 Δx→0，而是利用（4）式或（10）式的因果关系、已知的 υ 值和实测的偏转角 Φ 计算出准确的 r 值（此处r是间接测得的）。将 Δx→0 当作是，测准粒子位置的唯一途径，不但是错误的而且是办不到的 [因为，从（9）式可以看出要求 Δx→0 是要求曲率半径趋于零（或要求入射粒子与力源零距离接触），认为“只有当曲率很小（或要求入射粒子与力源零距离接触）时才算是测准了位置”岂不是很荒唐？从另一个角度看，当 Δx→0 时，缝就消失了，入射粒子有一定大小而不是质点，当缝窄至一定程度时，入射粒子就会被卡住或受到严重的随机干扰]。可见，把 Δx→0 当作测准粒子位置的唯一途径是自行设置测量的障碍。Δpx或psinφe趋于零表明的是粒子走直线，认为“只有粒子走直线才算测准了粒子的运动量”同样是荒谬的。在数理逻辑和实践中都是“不管路径弯曲得多么厉害，只要知道准确的曲率、线速度和质量就认为测准了动量”，动量值的测量精度并不与运动路径趋于直线的程度正相关。所以，认为 Δpx→0 （即被测客体趋于走直线）才算是测准了粒子的动量，是对动量测量准确度的误解。

3.1.5 影响“仪器对客体的影响不可忽略等同于影响不可预测”的观念

这种影响也是对主观介入观念的影响。“量子力学测量结果是仪器与被测客体相互作用的结果，不可能将共同的结果拆开”的悲观态度是产生“主观介入”观念的技术原因。“主观介入”观念的核心内容是“微观概念不再具有客观性，量子微观世界不会独立于主体之外”。在通常情况下，即使是知识量很少的人也知道“不可忽略”与“不可精确预测”是两个不同的概念，但是在量子力学中，许多资深学者也不自觉地认为“仪器对客体影响的不可忽略”一律属于“仪器对客体的影响不可精确预测”的范畴。在经典力学实践中，间接测量方法是常用有效方法。但在量子力学测量中，由于没有轨道概念，常常是“摸着了或碰着了”才认为是“测着了”，间接测量方式几乎无法使用。更有甚者将Heisenberg关系的单一统计意义与March的实证哲学相结合，从而沿着这种思路滑得更远——提出了“主观介入”理念。有人甚至由此得出“月亮在无人看它时确实不存在”的荒谬结论。

在将Heisenberg关系的非决定论意义当作唯一可用的前提下，就会认为在量子力学的测量中不能测出被测客体的独有的纯本体论的性质，量子测量结果依赖于仪-客相互作用：量子可观测量显示的是客体与观测仪器的相互作用的性质，量子可观测量只有在观测时才能有数值[2]。既然Heisenberg关系不能强硬地否认轨道运动，我们就不能否认仪器对客体的影响可根据单一因果关系准确预测的实验在微观世界适用。换言之，在微观世界中，我们也有可能同时测准粒子的动量和位置（在理论障隘消除之后，技术关键是建立实用的基本粒子模型）。只要我们不再受“没有轨道概念”的思想束缚，主观介入测量观就失去了赖以生存的土壤。总之，Heisenberg关系的决定论意义的发现动摇了“主观介入”测量观的理论基础。

3.1.6 影响“测也不准不测也不准”的观念

这种观念是将Heisenberg关系的适用范围扩大化（扩大到了不测量的任何时候）所造成的无可奈何之举。只要将Heisenberg 意义（非决定论意义）的Heisenberg关系的适用范围限定在有随机干扰的测量的范围内，认为只有决定论意义的Heisenberg关系才适用于一切无随机干扰的测量，且认定不测量时不一定有随机干扰，这种观念就不攻自破。

3.1.7 对微观粒子的波动性所具备的广延性与粒子性所具备的定域性之间的矛盾的影响

Heisenberg关系的决定论意义只能给解决这一矛盾提供一些启发和线索（例如，在可以使用轨道概念的启发之下，可以假设基本粒子是由广延性的波沿闭合路径传播构成的，原子、分子中的电子的运动轨道就是组成它的波的传播路径，从而使微观粒子的广延性与定域性得到了统一。详见第4章），而不能在不作进一步探究的前提下完全解决这一矛盾。

3.2 对若干实验和客观现状的解释的影响

本文不否认波-粒二象性，在否认几率诠释之前，原则上不排斥量子力学正统观念对实验现象的解释，只是在否认了几率诠以后，才必须调整对实验现象的解释。对于电子（双缝）衍射实验，或1998年用原子束做的“走哪一条路”实验（which-way，WW）[4,5]以及各种薛定谔猫态实验等，可以用粒-光效应（详见4.3节）和粒子的波动性解释。如果读者愿意，在随机干扰不可忽略时就可完完全全地回到正统量子力学。所以，对于其它实验，只要是正统量力学可以解释的在本文条件下也都是可以解释的。既然已经挣脱了“没有轨道概念”的思想束缚，对一些客观状态和已有实验现象就可以有与以前不同的解释。爱因斯坦当年设计的思想实验在上个世纪80年代都相继实现了，实验结果虽都支持量子力学，但又引出量子纠缠、量子隐态传输等一系列新问题，量子测量的实质、是否与相对论矛盾等问题也重新提了出来。本文得到的测不准关系具有决定论和非决定论的双重意义有可能为“在解释实验现象的同时避免那些问题”找到出路。

3.2.1云室中的带电粒子径迹的意义

讨论没有电磁场的云室中一个电子的径迹。一种云室径迹的正统意义为：云室中电子径迹的粗细是电子的位置不确定度，由ΔpxΔx＝h关系可知，因Δx很大而使Δpx很小（即承认在目前的测量精度范围内，电子是在走直线，其动量已经被测准了）。既然电子是在走直线，那么，比电子的大小大10万倍的云雾径迹那么粗的空间范围就不可能都是忒小的电子可能出现的地方（如果认为“是”则电子就不可能是在走直线。电子的大小被认为与对应的德布罗意波长相当，也与X射线波长相当，为10－10米的量级）。

①Heisenberg关系的决定论意义的发现，轨道概念可以用在量子体之中。②从被测电子的速度、电子径迹的长度和通过这段长度所花的时间可以看出电子在云室中走的是直线，肯定了电子是在做直线运动，就肯定了电子的直线运动状态很少受到干扰，不可能是在与电子云雾径迹粗细相等的通道中作不规则的曲线运动。③实际上，由于云室中的水分子很稀疏（与电子的大小比较而言）而且是电中性的，入射电子的动量很大，那个电子是以“雁过留声”、“机过留烟”的方式通过的，受到云室中稀薄分子的影响可以忽略不计。④云雾径迹的形成原因是带电粒子的电场引起了水（也许是酒精）的饱和蒸汽压降低，使那个电子路过的地点周围的过饱和蒸汽凝聚成小液滴。液滴首先在电子所在的点上形成，然后由这一点迅速扩大，有相当一部分云雾空间是在电子已经走开的情况下形成的（肉眼可见的部分都是），云雾的粗细正是电子的电场力所能影响的范围与事后扩大的范围之和的显示，而不是电子的中心可能到达的范围（在电子走开之后形成的云雾空间绝对不是电子可能到达的空间），更不是电子弥散的空间范围，电子只是在云雾径迹横截面的中心掠过（与无风的时候，喷气式飞机只是在烟道的横截的中心掠过的情况非常类似）。以上四种原因相互支持地表明云雾径迹的中心最有资格作为电子的真实运动路线，只要能找到电子云雾径迹的中心，就可认为测准了电子的位置。

带是粒子的电场对雾滴形成的影响程度以与距离的平方成反比的速度递减。由此我们不宜说带电粒子经常到达云雾径迹的边缘。正电子在云室中并不是很容易地与云室空间内的分子中的电子发生湮没。这表明带电粒子在云室中的运动不是随机的（若是随机的就很容易与分子碰撞而湮没掉）。

在Heisenberg关系的决定意义被发现之后，我们再也不需要用一些牵强附会的解释来迎合Heisenberg关系的单一统计意义了。不难发现，如果不把全部的云雾空间说成是带电粒子的位置不确定度，云室径迹所反映的事实就不符合非决定论意义的Heisenberg关系了，只要Heisenberg关系的非决定论意义“颠覆不破”、“放之四海而皆准”的神话堡垒被打开了缺口，非决定论意义的Heisenberg关系就不能作为量子理论的“一条普遍的基本规律”了。只要我们坚持公正的原则且使用逻辑武器，就不难分辨一种解释是否是为了保持某种理论的自洽而歪曲了事实。

3.2.2 对得布罗意波及实物粒子衍射实验的解释影响

严格的理论分析表明，德布罗意波 (de Broglie Wave) 的相速度为＝E/p＝c2/υ＞c，而相对论不允许有大于光速的实物。所以，德布罗意单色波是不可观测的[3]，在光速不可逾越的前提下，德布罗意波只能是一种虚拟波或不紊扰波动情况。能够观测的最多只能是德布罗意波包。两个波包之间产生干涉必然得到不清晰的干涉图样。所以，清晰的电子衍射图样不可能是由波长符合 λ=h/mυ的单色德布罗意波形成的。理论上不可能而在实验的解释上又认为是可能的，显然非常矛盾。在Heisenberg关系的决定论意义发现之后，对于实物粒子的衍射实验，我们就有更多的理由不选择“德布罗意波发生衍射”的解释。对于德布罗意波的本质将在其他文章中详细讨论。

3.2.3 对Quantum Decadence起因的解释

量子力学哥本哈根（Copenhagen）解释认为，动量和坐标之间的Heisenberg关系是引起 Quantum Decadence 的一个重要原因。但是，最近德国 Rampe 小组的冷却原子 Bragg 散射实验表明，Heisenberg关系不是Quantum Decadence 的唯一起因，而测量仪器和被测系统通过相互作用，形成的量子Entangled State 是问题的核心。在他们的实验中，原子质心的动量扰动，可以被降低到忽略不计的程度，只须用原子的内态标记原子的空间路径，原子的干涉条纹便消失了。Rampe 小组的冷却原子布拉格散射实验从一个侧面表明，Heisenberg关系可能是“粒光效应”的体现，而不是由“主观介入”引起的。Rampe 小组的冷却原子Bragg 散射实验进一步说明 Copenhagen 量子力学解释的局限性，Mach 的实证哲学与Heisenberg关系的非决定论意义相结合是导致量子力学理论必须引入“主观介入”的主要原因，也是量子力学解释产生的原因。Heisenberg关系的决定论意义的发现无疑支持Rampe小组的实验结论。

3.2.4 对几率诠释的影响

几率诠释的产生原因是“Heisenberg关系仅有非决定论意义与对电子的内部结构缺乏认识的组合，形成了‘核外电子没有确定的运动轨道，只有统计意义’的观念”。现在既然发现了Heisenberg关系的决定论意义，量子体系中没有轨道概念的观念也被动摇了，我们就有更多的理由恢复 的原有意义——正比于能量密度（或单位体积内的电场强度），而不再用它表示几率密度。第4章建立的模型

3.2.5 对贝尔不等式及其验证实验的解释的影响

在贝尔不等式 (Bell’s inequality) 的推导中，有一个隐藏在概率论后面的假设——概率遵循迭加原理。可是这一假设与量子力学的形式体系相矛盾从而与实验实事相矛盾。贝尔不等式被实验否定只不过再次证实了这种矛盾，与定域实在论完全无关(即不能否认定域实在论) [2]。所以，阿斯贝(Alaine Aspect) 1982 年在巴黎大学所做的实验并不能严格地证实微观粒子的模糊世界只是在观察时才变成具体的实在，在没有观察时微观粒子只是一个幽灵。再说在验证贝尔不等式的 16 个实验中有2个是肯定的，占总数的 12.5%。在验证实验中并不符合“少数服从多数”的数量规则，一个正确的实验可以否定一

大堆不正确的实验。谁能肯定那个 12.5% 的概率只是意外而那87.5%的结果不能用其他的理论解释呢？我们为什么要轻易地放弃严谨的作风，轻率地依附 Copenhagen 学派，从而极力否定域实在论的有益尝试呢？

这类实验的受试对象是光子，光子有着特殊的对称性，不能作为微观粒子的全权代表。

3.3 对测量理论的影响

现有的量子力学测量理论以“实验客体受到实验仪器的不可忽视和不可准确预测的干扰”为基本前提。其理论根据之一就是非决定论意义的“Heisenberg关系”或“不确定度关系”。在发现了Heisenberg关系具有决定论和非决定论的双重意义之后，现有的量子力学测量理论有必要作些修正。下面用一个图形来表示测量理论的主要内容。

在Heisenberg关系的决定论意义被发现之后，就少了一种“主观介入”的实验理论。以上每种类型又可分为间接测量和直接测量两大类。在实际测量中，可将不同类型的测量方式混合使用。但是在量子力学中，受“主观介入”观念的影响，人们很少承认间接测量结果。

4 基本假设、预言和验证实验设计

4.1 本文的唯一基本假设——光元子沿闭合路径传播构成定域粒子

克服广延性与定域性之间的矛盾的最好方式之一是假定波沿一个闭合路径传播。以前也曾有人提出过质子电子尺寸的闭弦模型，但因缺乏相应的理论机制而被放弃。现在周海麟提出的周氏力[6]可望成为质子电子尺寸的闭弦稳定存在的理论依据。Heisenberg关系的决定认意义的发现又给了我们一些启示。假设一个圆偏振光量子由k个更小的光元子组成，同种光元子之间就存在周氏相互吸引力。将非线性周氏力的线性近似取为F=—e2/4πε0 R2，就有

e2/4πε0 (2r)2=(m/k ) (c2/r) . (18)

（18）式中 m 为电子的质量，且 2mc2 =hν, 2πr=λ=c/ν. 故 k=4ε0 hc/e2=2/α≈274，即一个自由电子由 274 个光元子连接着并沿闭合路径传播组成。由惠更斯原理（Huygens作图法）可知，那 274 个光元子可优先成为次级子波源。当自由电子受外场干扰之后，其中的 274 个光元子中的每一个都可复制出波长与母波相同的 n2 （n=1，2，3…）个次级子波（Huygens 原理的这种表现可以通过求解波动议程得到，所以它不能算是基本前提）。一个基态氢原子的结构是：氢核处于由 274 节次级子波围成的一个圆的圆心之上，基态电子闭弦半径（记为rb）为 rb =274λ /2π. λ是能量恰恰为阀频的 γ-量子的波长，数值为 1.2131548×10－12米。自由电子半径为：1.2131548×10－12÷2π=1.9×10－13米。所以 rb =0.529×10－10米，与玻尔半径数值吻合。这也阐明了氢原子中电子的德布罗意波是由 274 节次级子波组成的一拍（若令274λ =λb，λb就是德布罗意波的波长，德布罗意波就是虚拟波）。

上述基本假设可完全取代玻尔（Bohr）氢原子理论是显而易见的。它的另几个好处是：①可替代现有量子力子中五个必要的基本假设； ②可成功地解释光子-电子相互转变的实事，改变了量子力学与基本粒子内部结构完全无关的局面； ③触及精细结构常数、电子自旋和德布罗意波的本质。即使周氏力的依据不足，能用一个假设代替一组（至少五个）基本假设也是值得重视的。

本文的基本前提是“光元子假设”。可以根据Heisenberg关系的决定论意义重新设计一些实验用于验证正统量子力学思想和本文的观点。解决光元子假设与现有的“标模型理论”之间的冲突不是本文的任务。本文只是展示光元子模型在量子力学中的成功应用。

4.2 根据基本假设所作的预言及其验证实验设计

根据本文提出的电子结构模型可以推知：圆偏振光的电磁场矢径的旋转方向决定它表现出两种不同的极性；基本的圆偏振光光线会在强磁场（或电场）中偏转；基本的圆偏振光会像静电场一样使导体产生感应电荷；单一极性的高能圆偏振光可以产生单个的电子、质子（或正电子、反质子）；电子对撞有可能撞出极性相同的圆偏振光；高能圆偏振光在云室、气泡室或火花室中可能产生径迹。可以设计出验证这些预言的实验方案。

4.2.1 光电场感应验证实验

将一块导体片的两端用一块灵敏度很高的电流表连接起来,再让导体片沿一定的方向在圆偏振光的电场空间中移动, 观察是否有感应电流产生，并检验圆偏振光是否有两种极性。

4.2.2 圆偏振光线在磁场中偏转和圆偏振光子在云室中的径迹的验证实验

让高能圆偏振光通过带有磁场（或电场）的云室、气泡室或火花室，观察径迹及其偏转情况。

4.2.3 圆偏振光的衰变实验

让能量超过阀频的圆偏振光子掠过重核，搜索它转变成的电子或正电子。

4.2.4 非正常电子湮没实验

利用对撞机证电子-电子（或正电子-正电子）对撞，能量分为＜1800m0c2和＞1800m0c2两个区域（m0为电子的静止质量）。观察是否有圆偏振光产生。

4.3 检验“粒光效应”的实验

微观粒子的衍射除了由波动性引起之外，还可以由“粒光效应”引起。所谓“粒光效应”就是指高速粒子在穿过一定的障碍时，导致光子产生的现象（与光电效应的过程相反）。它包括“韧致辐射”、“诱导辐射”和“光平衡移动”等。在做粒子衍射实验时，狭缝和靶（感光底板）都处于黑暗的体系之中，狭缝也是一个黑体辐射源，只是当没有外界干扰时，其辐射强度很低。当粒子高速穿过狭缝时，就会诱导出更强的电磁辐射。这就是“诱导辐射”。实物粒子撞击原子、分子中的电子而产生光子的机理有可能是入射粒子把原子、分子中的低轨道电子撞离原来的位置，该电子跃迁回原来的位置就发出电磁波。“光饱和原理”也是“粒光效应”的产生原因之一，它的意思是：每个近似的封闭体系都是近似饱和的蓄光体，只要饱和蓄光体受到了外来干扰（原平衡受到了破坏）就会发射出与干扰源的动量相当的光子。部分非封闭状态的物体也具有饱和蓄光体的性质。只要我们将组成缝的物体看作饱和蓄光体，λ＝h/mυ 成立，（19）式和（21）式也近似成立。 要用更精确的实验证实一次具体的实物粒子衍射是符合哪一个公式。

对于“X射线的产生”（目前认为是“韧致辐射”）这种情况。所产生的电磁波的波长有如下所述的规律。X 光机的应用实践证明高速电子打在一个斜面上可产生X射线。 所产生的 X 射的最小波长为：

λmin＝hc/Ek＝h/Δmc. (19)

中高速电子不可能撞到斜面上的原子核上，打在斜面上的电子是与斜面上的电子相撞。高速电子打在晶体上会以相同的机理产生X 射线。戴维孙和革末 (Davisson and Germer) 利用电子束穿过镍单晶形成的衍射图样，只有在严格地排除了“是由电子撞击形成的X 射线等原因造成的”（即严格排除了 “粒光效应”）之后才能认为它证实了德布罗意波。因为 (19) 式与λmin＝h/mυ在一定条件下 (如电子速度很高) 很接近，电子打在晶体表面上首先是与电子碰撞。

任何晶体中的原子核都是处于电子云雾之中，电子束流穿过两 Bragg 平面之间的缝都必须与缝中的电子相撞。入射电子就最有可能撞出动量相当的光子来（原因是发生韧致辐射或被撞离基态的电子跃迁或其他），撞出的光子再发生衍射便形成了衍射图样。所遵守的动量守恒方式之一如下：

γmυ1―γmυ2 = hν/c. (20)

考虑到 c =λν，(20)式变为：

(21)

式中 υ1 是入射电子速度，υ2 是出射电子速度，hν/c是撞出的光子的动量。.上面的衍射实验能严格、精确检验Davisson and Germer实验是电子的衍射还是光子的衍射，衍射是严格符合 (19) 式还是 (21) 式还是 ＝h/ mυ。

一个光子穿过双缝，先是根据惠更斯 (Huygens) 原理产生多个次级光子，之后才是次级光子之间相互干涉。这种解释是符合逻辑的，每一步都有清晰的物理图象，不需要认为光子在穿过狭缝时变成了不合逻辑的幽灵。人们已经发现，即使让电子一个接一个地（序贯地）穿过狭缝也能得到衍射图样（将电子的次级散射效应降低到可以忽略）。若认为此时的电子是完完全全的波，则它在到达缝时也会根据 Huygens 原理使每个电子都变成多个次级电子（亚电子），然后是亚电子之间产生干涉。电子序贯地穿过双缝形成的衍射图样的客观性决定了推论中的亚电子必须是客观的。可是，高能物理实验却没有发现电子可以分为更小的更基本的粒子，即高能物理实验事实不允许亚电子存在。这样我们不得不认为亚电子是幽灵或者电子在穿越缝的过程中是幽灵。如果认定自然界没有幽灵，那么“电子衍射是由于电子表现出了波动性”的现有解释就是不成功的。换言之，我们不能说电子衍射实验严格地证实了电子在穿缝过程中表现出了波动性。

由于过去在做的实物粒子衍射实验时没有认真地考虑“粒光效应”，因此有必要重做1927年汤姆逊（G. P. Thomson）做过的带电粒子序贯地穿过狭缝的实验，重点检测让它们逐一打在感光靶上所表现出来的特性[靶可以是闪烁计数器、切伦科夫（Cerenkov）计数器和核乳胶]，如果每个粒子打在靶上分别体现出的都是“点”的性质，则该粒子在穿过缝时就并不是像惠更斯原理所描述的那样形成了次级子波，且发生了子波之间的干涉，实物粒子的衍射图就不是波-粒二象性造成的。进一步地，在电子衍射实验的缝与靶之间增加一个横向的电场（或磁场），促使电子束流偏转，如果电子束偏转了而衍射环没有位移（仅发生衍射图变形或变模糊），就充分肯定了衍射完全是由光波造成的而不是粒的波动性造成的。而最有可能是由“粒光效应”造成的。

对于质子、原子、分子和较重的离子等实物粒子的衍射，如其说是波动性的体现，还不如说是粒光效应的体现。对于粒光效应，我们只能选择它的种类而不能完全否认它的存在。我们有什么充足的理由否认实物粒子在穿过狭缝时会产生可观的粒光效应呢？

4.4电子掠过裸核表面的实验

用激光将一个（或一对）质子固定起来，让电子掠过质子的表面（或穿过两质子之间的空间），测量电子射线的偏转角，用以检验（5）式和（11）式，并作为同时准确测量粒子的动量和位置的范例。

5 仅以一条假设为前提建立量子力学体系[7]

这就是利用基本粒子结构模型美化量子力学的尝试。如果的确能完成本章题名所述的工作，那么，本文中的处理方式对于美化量子力学和量子力学的教学工作就是很有意义的。谁也不肯定现在所下的科学结论（特别是对物质结模型的认定）都是最后的定论。我们最好不要轻易地否定任何一种很有用假设。

上节的基本假设说的是电子是由圆偏振光量子围成的。在势场中波的能量改变，但波的形式不变。故自由电子中的波和势场中的电子都可用下式描述。

(22)

对(18)式作适当的偏微分,可得

(23)

　 (24)

(25)

(26)

既然核外电子是一种首尾相接的波（Huygens 原理对它起作用的基本的圆偏振光波），就可认为电子的电荷均匀地分布在半径为rb 的相轨线上。这样，氢原子基态的势能函数为

Ep =－e2/4πε0=－e2/2ε0λb. (27)

在平衡系统中, 维里定理 (Virial theorem) 成立,并考虑到 α=e 2 /2ε0hc 我们有

Ek=－Ep /2=hαc/2λb = (ћ2/2m) (2π/λb)2. (28)

将（28）式代入（24）式，得

(29)

考虑到 Ek =E－V，（29）式变为

. (30)

比较c=λν、（28）、（25）、（29）四式，可得

(31)

（30）式和（31）式都是薛定谔（Schrödinger）方程。都是哈密顿（Hamilton）算符：. 经典的动量-能量关系为 p2=2mEk=(mυ) 2 . 将它代入 (28) 式，可得 2mEk =(h/λb) 2=p2和p=h/λb. p=h/λb是已命名的德布罗意关系。这就证实了德布罗意波是虚拟波（虚拟其波长为n2×274倍的真实波的波长），德布罗意关系不再是一个独立的假设而是根据本文前提严格导出的关系。将德布罗意关系代入 (23) 式，可得

(32)

将 Ek =P2/2m 代入 (29) 式, 可得

(33)

(32)式和(33)式分别给出了动量算符和动量平方算符。

用λb替换λ, 选择（28）式中的Ek=hαc/2λb 的形式代入（23）式，可得

(34)

将Ek=E－V 代入（34）式，可得

. (35)

(35)式就是势场中的狄拉克（Dirac）方程。

将 代入 (21) 式, 可得

. （36）

(34)－(36), 可得

(37)

由于相对论动能与总能量之差为 mc2, 因此,只要我们将E 中的质量取为 ±m, (37) 式就可变为

. (38)

式中β=±1. (38)式就是自由粒子的狄拉克方程.如果宇宙中存在对称的正能量世界和负能量世界，那么，在正能量世界中负能量和负质量没有意义, (36)、 （（37）两式分别只能是

(39)

和 (40)

将(或) 代入 (26) 式,

. (41)

(41)÷c2－ (33), 可得

. (42)

(42)式就是克莱因-哥登 (Klein-Gordon) 方程。当m=0时，（42）式变为

. (43)

(43)式是达朗贝尔（D′Alembert）方程。

（18）式、（27）式和（28）式是使用了轨道概念的表现，（22）式是使用了波函数的表现。德布罗意关系、薛定谔方程、狄拉克方程及量子力学逻辑体系是同时使用轨道概念和波函数的产物。在同时使用轨道概念和波函数的前提下，对于非多粒子随机运动的情况，几率密度正好等于场能密度。只有在核外电子定域的情况下几率诠释才在观念上不正确，但对能量的计算结果仍然是正确的。可见，几率诠释仅在描述无随机干扰的体系的结构方面不准确，但在能量统计方面是可用的。本文不否认统计解释。

6同时使用轨道概念和波函数的量子力学计算实例[8]

根据第4章默认的电子结构模型可知，1个（或数个）未受随机干扰的核外电子的相轨线是定域的。由此，我们也知道一些小分子的结构。例如氢分子离子的结构是一个相轨线环的两侧各有一个氢核（见图1）。它也是一个力学平衡系统，力学平衡状态方程为

(e2/L2) cosθ=e2/Re2 . (44)

这个方程的解是θ=50°5710". H2+ 的总势能函数为V=－2(e2/L2)+e2/Re=－1.2603(e2/L). 以类氢离子计算,相应的能量为E=－19.797eV. H2+ 中电子的势能函数为Ve=－2e2/Re=－2sinθ(e2/r)=－1.553(e2/r).同样以类氢离子计算,得相应的能量 Ee=－32.826eV. E与Ee 之差为核间相互作用能：2e2/Re =E－Ee, Re=2.0899a0≈1.10×10－10米。 H2+ 的离解能为De = 19.799eV－13.606eV ≈ 6.2eV. 对应的实验值为 Re=1.06×10－10 米和 De=2.79eV. 如果考虑到电子和核的自旋相互作用，误差可望消除。

氢分子（H2）的力学结构与 H2+ 的很相似，不过两核之间的相轨线是双电子闭弦。体系的力学平衡状态方程的解为θ=π/3. 体系的总势能函数为V=－(4e2/L)+(e2/Re)=－1.5(e2/L)－1.5(e2/L). 以两个类氦离子计算，相应的总能量为 E =－1.52(e2/2a0)×2=－61.227eV. H2 中纯电子的势能为Ve=－(4 e2/L)=－(2sinθ)(2e2/r) =－1.732(e2/r)－1.732(e2/r). 以类氦离子计算,相应的电子能量为Ee =－2×1.7322 (e2/2a0)=－81.636eV. 同理我们有： e2/Re=E－Ee, Re=1.333a0≈0.71×10－10米。既然 H2 基态中的双电子与 He 原子基态中的双电子的环境相同（n =1, Z =2）,那么，H2 中电子之间的相互作用能也应为 29.829eV. 所以 H2 的离解能为 De=61.227eV－29.829eV－13.606eV×2≈4.2eV. 相应的实验值为： De=4.75eV, Re=0.74×10－10米。

He2+ 的结构与H2+ 非常相似。当基态氦原子发生电离时，逃离的电子所感受到的核电荷数（有效核电荷数）可以根据电离能计算出来（假设内层电子未重排）。对于第一级电离而言，计算公式为I=Z*2(e2/2a0)。将I=24.587eV代入其中，可得 Z* =1.3443.将He2+ 当作有效核电荷数为1.3443的点电荷。我们可以得到力学平衡状态方程的解为θ=45.9527°. 体系的总势能为V =－(2×1.3443)e2/L + (1.34432)e2/Re=－1.3889(e2/L). 以类氢离子计算，相应的总能量为E=－1.38892e2/2a0=－26.249eV. He2+ 中成键电子的势能为Ve=－(2×1.3443)e2/L=－(2×1.3443sinθ)(e2/r)=－1.9325(e2/r), 以类氢离子计算,相应的成键电子能量为Ee=－1.93252e2/2a0=－50.812eV. 两个He2+离子之间的相互作用能为 (1.344432) e2/Re =50.812eV－26.249eV =24.563eV, Re=2.00192a0 =1.06×10－10米。 He2+ 的离解能为De=－E－I1 =26.249eV－24.587eV=1.662eV. 相应的实验观测值为：Re=1.08×10－10米，De=3eV。

Li2 的结构与H2 相似，不过两成键电子处于n =2 的能级之上。锂元素第一电离能为 5.392eV。所以，锂原子中 2S 电子感受到的有效核电荷数为 1.259 (即5.392eV=Z*2/22, Z*=1.259)。将 Li+ 原子实当作有效核电荷数为1.259的点电荷，力学平衡状态方程的解为θ=57.3229°. Li2 的总势能为V=－(4×1.2592e2/L)+(1.2592e2/Re)=－3.56812(e2/L). 以类氦离子计算，相应的总能量为E =－21.653eV.成键电子的势能为Ve=－4×1.259(e2/L)=－(4×1.259sinθ)e2/r =－4.2391(e2/r).以类氦离子计算相应的能量为Ee=－(2.11952/22)(e2/a0) =－30.562eV.两Li+之间的相互作用能为(1.2592e2/Re)=E－Ee , Re=4.842a0≈2.56×10－10米。对应的实验观测值为Re=2.67×10－10米。

本文在减少前提、建立波动方程（即量子力学体系）、四个分子的量子力学计算、德布罗意关系的导出、对轨道磁矩、轨道角动量和光子电子相互转化的解释多方面取得了令人满意的结果。如果是不正确的理论，得到这种结果的概率将是非常低的，本文的处理方法的成功不可能只是一种巧合。“标准模型理论”仍然将电子当作基本粒子，而本文中的电子模型是下一个层次的结构模型，所以，“标准模型”理论不能否认光元子假设。更不能否认这一假设在量子力学中的成功应用。

7 同时使用轨道概念和波函数的优点小结

归纳起来，本文介绍的处理方式具有如下优点：

7.1 将定域实在论的因果描述和统计描述统一于对同一客体的描述之中

即使是在微观体系中，决定论意义的确定度关系仍然可用于无随机干扰的理想状态的理论描述。它的导出表明了，Heisenberg关系不能决定“微观体系中只存在随机干扰的状态而不存在无随机干扰的状态”。以前是由于没有这种“描述微观体系中无随机干扰的理想状态的理论方法”人们迫不得已地认为：在微观体系中，凡是干扰都是随机的，讨论无随机干扰的状态没有意义。决定论意义的确定度关系导出之后，这种状况自然地得到了改观。

既然Heisenberg关系的单一统计意义是“随机干扰不可忽略的前提下，f(q, υ)≈1的特例”，其非决定论意义的适用范围被错误地扩大了，“测不准原理”就不可能是普适的原理，定域实在论描述与统计描述就是协调的。它也决定了：凡是有可观随机干扰的测量结果或受试对象的波动性突出的测量结果必然符合统计解释；允许随机干扰消除得可以忽略的测量结果符合定域实在论的解释；受试对象的波动性不够突出或随机干扰消除得不彻底但相对较弱的实验结果可同时采用统计解释和定域实在论的解释。

认为核外电子是德布罗意波，而波一般具有统计性质，因此可利用与波函数对应的统计规律描述核外电子。波的相轨线在任何情况下都可以看作是构成波的能量实体的运动轨迹，因此在描述核外电子时又可以采用定域实在论的思想方法。对于单电子平衡体系而言，用统计方法可以得到场能的密度分布和其它物理量的本征函数和本征值，用定域实在论的描述方式可得到体系的力学平衡结构和自旋（或轨道）运动角动量等。任何体系只要出现了随机过程就可以采用统计描述；矩阵力学与波力学相容的潜在本质是统计解释与决定论解释相容。

7.2 增强了量子力学体系的逻辑性

只要读者注意到第4节和第5节，就能发现不必使用五个基本假设就可导出量子力学的一整套基本方程，在导出相对论性量子力学基本方程时也不必增加一些直觉原则。减少了前提而又增强了逻辑性就是美化了量子力学。

7.3 扫除了量子力学与相对论相结合的部分逻辑障碍

由于非相对论性或相对论性的量子规律和状态分别是伽利略或庞加莱(J. H.Poincaré)不变的，并不是广义协变的，因此加速运动与匀速运动的量子系统并不等价。这就是相对论与量子力学之间的重大矛盾之一（矛盾1）。所以，联合国教科文组织在《1998年世界科学报告》中指出：“爱因斯坦的理论（相对论）和量子力学是二十世纪的两大学术成就，遗憾的是，这两个理论迄今为止被证明是对立的。这是一个严重的障碍。”

Heisenberg 关系也可表为 ΔpΔt～h/c由于c是常数（光速），而相对论不允许有超光速的运动，因此由 ΔpΔt～h/c可看出，测准动量必须花无限长的时间[9]。就是说，在Heisenberg 关系的非决定论意义的限制下，在相对论性理论中，对动量进行任意精确而快速的测量在原则上是不可能的（矛盾2）。如果具有负几率的波函数相当于存在反粒子，那么在测量高速电子坐标的过程中就不可避免地要产生电子-正电子对。这类新粒子不能通过过程本身来进行探测，这就使得对高速电子进行测量变得毫无意义。朗道得出了下述结论：非相对论性量子力学的全部表述中，波函数ψ(q) 不能以不可观测的信息的运载者的原来意义出现（矛盾3）。

“波包缩扁”显然是一种超距作用，与相对论假设矛盾（矛盾4）。

（12）、（13）、（14）、（15）和（16）直观反映的 ΔpΔx～h 的决定论意义表明，测准动量p（或Δp），只需在已知入射速度（或动量）的情况下测准偏转角φ 就行了。这样，Δp不必趋于零, Δt就不必趋于无穷大。矛盾2就这样解决了。在导出狄拉克方程的过程中，本文倾向于认为负能量和负质量是负能量世界中的物理量，负几率也就不与反粒子对应。在正能量世界中能量、质量和几率只能取正值，故矛盾3不会出现。即使实测时产生了反粒子也就不表示理论上有障碍。解决矛盾1的方式是否定广义协变原理的普适性。

7.4 将电子的波-粒二象性阐释得更加清楚

在本文之前，一般认为波和粒子是一对矛盾的实体，人们只承认微观粒子具有波-粒二象性的实测结果而不能给出决定波-粒二象性的具体而清晰的物理图象（结构）。本文认为核外电子是闭合路径传播的波，这是决定可以同时使用轨道概念和波函数的关键，也就是能阐明波-粒二象性的具体模型。首先肯定微粒是波，然后用波沿一个较小的闭合路径传播来说明波的能量可局限于较小的空间之内（即构成了定域实体）。波沿闭合路径传播的确是统一波的延展性和粒子的定域性的巧妙方式。有什么理由说大自然不选择这种巧妙的方式呢？波动性和粒子性统一于一个微粒之上是客观事实，在没有找到其它解释方式之前为什么不接受“波沿闭合路径传播”这种解释呢？在这种解释表现出了许多优点之后仍然不接受它，很有可能是脑中的陈旧观念在作怪。测不准确性关系的决定论意义发挥作用时，根本不存在“波包缩编”问题。即使是出现了随机干扰，也不会出现“弥散”现象，“波包缩编”现象也不存在。

7.5 能弥补正统量子力学不能从动力学上解释原子、分子的稳定性的不足

如果真像几率诠释所认可的那样，H2+ 中的那个电子可在两氢核附近各处出现，那么，在大部分时间内点电子都处于使两氢核偏离实测平衡位置的状态。也就是说，从动力学上考虑，在大部分时间里H2+ 都有偏离核间距为1.06×10－10 米的趋势.可见,如果电子是点粒子而在核外空间中随机地出现，那么，从动力学上看，H2+ 在大部分时间内就是不稳定的。H2+ 稳定只是热力学上的统计平均结果。如果像本文所述的那样电子波在两个氢核之间沿一个圆周传播，则H2+ 体系既可以达到力学平衡又可以达到能量密度在两个氢核之间最大的状态（对应于几率诠释的“几率密度”在两氢核之间最大的状态）。对于单个的氢原子而言，其轨道磁矩和轨道角动量不应是统计平均（轨道磁矩和轨道角动量有确定值表明了核外电子动的非随机性）。

7.6 使量子力学更协调地包含经典力学

尽管现有的正统量子力学在取势能函数等少数几处采用了经典力学的处理方式，但在观念上,现有的正统量子力学是完全排斥经典力学的（因为经典力学属于定域实在论的范畴而正统量子力学是非决定论的统计力学）。在本文前提下，只要认为电子的电荷和质量均匀分布在闭合的相轨线上，经典力学方法就是完全适用的（但同时又可采用波函数的统计描述）。本文的思想观念恰好可以说明在量子力学中为什么可以用V∝e2/r的经典形式建立势能函数。可见，本文使量子力学中的观念和方法更加协调。

7.7 实现了定域实在论与统计决定论的完美统一

现有的量子论对运动中的电子等基本粒子，只能在定域实在论描述和统计描述二者之中选择一种，而不能同时用这两种描述方式描述同一运动粒子。本文论证了决定论意义和非决定论意义，可统一于同一事物（如Heisenberg关系）之中，也就肯定了可将定域实在论描述和统计描述同时作用在同一客体之上。例如，可在用经典力学描述云室中的高速粒子的同时使用统计描述而计算出该粒子受到微弱干扰造成的位子不确定度。现在，高精密度实验恰好证实了即使是宏观物体，也有测不准的成份。这在本文看来是很正常的：如果随机干扰的力量比惯性运动力量小四个数量级，那么，统计方法描述的空间不确定范围必在比牛顿定律描述结果低四个数量级的范围之内。宇宙背景辅射、人间噪声等都可成为随机干扰的动力源。总之，最新的关于测量的实验结果支持本文的结论（因为“大物体在特小范围内也测不准”的最新实验结果需要定域实在论描述与统计描述相容的理论解释）。由轨道运动方程（规律）导出了不确定度关系可使经典运动规律的适用范围从宏观领域延伸到微观领域。本文从逻辑上认可了“核外电子既是粒子又是波”在一定条件下可同时采用波动描述和定域实在论的描述。另一方面也能将测不准原理的适用范围从微观领域扩展到宏观（或经典运动）领域。这一优点决定了本文不是倒退到经典定域实在论的老路上去，更不是在完全的统计决定论的道路上走得更远，而是站到了“定域实在论与统计决定论相容”的高度，使九泉之下的爱因斯坦和波尔可以握手言和。

8 结束语

按理说，非决定论意义的 Heisenberg 关系是量子论的基本原理，扩展了不确定度关系的意义对整个量子论就有重大影响。正统量子论及其解释不是完全不正确而是偏离了辩证的轨道。本文的目的就是想使量子力学及其解释系统变得更加辩证，且通过发现 Heisenberg 关系还有决定论意义和提出一条假设而办到了。本文有参考价值的主要原因是“改进量子力学解释系统但不否认正统量子论的成功应用”，而正统量子论的特点恰恰是内在的逻辑性欠佳但应用相当成功。也就是说，本文介绍的思想可以做到扬其长而补其短。

基础研究一般可分为两大类：甲）在已有的框架之内完善和发展已有的理论；乙）突破甚至重建理论框架。甲类易引起共鸣也就易于被接受，乙类需要读者改变观念，一般难以被接受（历史上的科学蒙难就是这个原因）。本文开拓了新的思维空间，因此说它远离前沿是不正确的。波为什么要弯曲而沿闭合路径传播是需要解释的和验证的。本文基本假设可预言：波长远短于测量空间的光线（特别是圆编振光线）在特强非均匀电磁场中会发生偏转（或表现出类电荷特性）。日本学者内田秀男的实验应该受到重视。

狄拉克曾明确指出:“我认为很有可能在将来某个时候，我们会得出一个改进的量子力学，使其回到决定论。只有放弃某些基本思想为代价才能办到，而这些基本思想我们现在认为是没有问题的。”[10]本文介绍的工作就是将粒子性理解为所研究客体非全域弥散的存在区域的定域性，从而将量子力学改进成了决定论和非决定论连通统一的理论，但不是完全回到决定论。人们不会忘记，测不准原理与经典运动规律相容正是人们在测不准原理发现之初的强烈愿望。

参考文献

[1] 涂润生. 测不准关系具有决定论和非决定论的双重意义[J], 山东师大学报(自然科学版)，

1999. 14(3): 64~65.

[2] 潭天荣. 量子力学实在论并未失败［J］，武钢大学学报，1995，7(4): 61~69.

[3] R. T. Weidner, R. L. Sells. Elementary modem Physics [M]. New York: Allyn and Bacon, Inc. 1980.

[4] 倪光炯，陈苏卿. 高等量子力学[M]. 上海：复旦大学出版社，2000

[5] Dürr S, Nonn T, Rempe G. Nature, 1998, 395: 33; Phys Rev Lett, 1998, 81: 5707

[6] Zhou Hailin. Binding Force in Wave-Particle Interaction [J], Nuclear Fusion and Plasma

Physics , 1998.18(1): 11~16.

[7] 涂润生. 一种美化量子力学的方案[J] ，山东师大学报(自科版). 2000，15(1)：31~33.

[8] 涂润生. 一种简洁的量子力学描述方式[J]，宁夏工学院报(自科版). 1998, 10(1):117~123.

[9] 朗道. 量子力学：理论物理简明教程Vol.2[M].北京：高等教育出版社，1990，231~233.

[10] P. A. M. Dirac. Direction in Physics [M]. New York: John wiley, 1978.

The Scientific Significance of Uncertainty Relation And Classical Law to Be Compatible ：The Must Result that Uncertainty Relation Has Determinism Significance

By Tu Runsheng

（128 Huangzhou Avenue, Agency of Product Quality Inspection in Huanggang City, Hubei Prcvince, CHINA）

Uncertainty relation has the dual significance of determinism-indeterminism. It can improve the explanation system of quantum mechanics and can beautify the logical system of quantum mechanics (can reduce the premise and do not need those intuition imagine when relativistic quantum mechanics is established). Owing to uncertainty principle and classical law excluded each other to be changed into forgiven each other, therefore we can both using the method of classical mechanics law in quantum mechanics and use the uncertainty principle in classical mechanics, and under given conditions we can use orbital concept and wave function at the same time. It is the ironclad evidence to be no different meanings that uncertainty relation can obtained by strictly analysis can indicate: both available experiment and theory can’t strongly testify that the particles in quantum system are the ghost whose true face to be showing for me only when it is observed. If above thinking and the latest experimental result obtained by Aspect etc are contradictory, the source of the problem is come from the explanation for Aspect’s experiment.

Keywords: New significance of uncertainty relation, Explanation system of quantum mechanics, Classical orbital concept, Phase-rail-line, Photo-atom.

PACS：03. 65. -w, 03. 65. Ud, 05. 30. -d, 03. 65. Pm, 01. 70. +w