谢尔宾斯基三角形

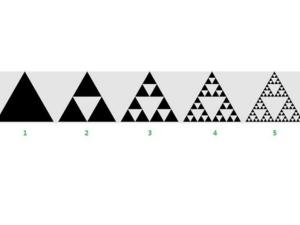谢尔宾斯基三角形的绘制1.取一个实心的 三角形。（多数使用等边三角形）

2.沿三边中点的连线，将它分成四个小三角形。

3.去掉中间的那一个小三角形。

4.对其余三个小三角形重复1。

取一个正方形或其他形状开始，用类似的方法构作，形状也会和谢尔宾斯基三角形相近：

1.用随机的方法（Chaos Game），都可得到谢尔宾斯基三角形：

2.任意取平面上三点A,B,C，组成一三角形

3.任意取三角形ABC内的一点P，画出 该点

4.画出 P和三角形其中一个顶点的中点

5.重复1

下图展示了 曲线如何逼近谢尔宾斯基三角形。

这条曲线以L系统来记述为：

变量: A , B 常数: + , - 公理: A 规则: A → B-A-B B → A+B+A A,B ： 向前

- ： 左转60°

+ ： 右转60°

谢尔宾斯基三角形先作一个正三角形，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色三角形代表挖去的面积，那么黑三角形为剩下的面积（我们称白三角形为谢尔宾斯基三角形）。如果用上面的方法无限连续地作下去，则谢尔宾斯基三角形的面积越趋近于零，而它的周长越趋近于无限大（如图）。

若设操作次数为n（每挖去一次中心三角形算一次操作）

则剩余三角形面积公式为：4的n次方分之3的n次方

将边长为1的等边三角形区域，均分成四个小等边三角形，去掉中间一个，然后再对每个小等边三角形进行相同的操作得……，这样的操作不断继续下去直到无穷，最终所得的极限图形称为谢尔宾斯基垫片。谢尔宾斯基垫片的极限图形的面积趋于零，而小图形的数目趋于无穷，作为小图形的边的线段数目趋于无穷，实际上是一个线集。操作n次后

边长r=(1/2)n，

三角形个数N(r)=3 n，

根据公式N(r)=1/rD，3n=2Dr，D=ln3/ln2=1.585。

所以谢尔宾斯基垫片是1.585。

它比普通的一维直线占据了更多空间，但还是没有二维正方形占据的那么多，可以用等比数列的只是求出他的面积是0。