封闭类时曲线

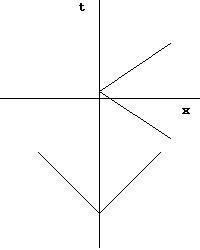下方光锥是平直时空中典型的光锥模样——所有包含在光锥里的时空坐标具有较迟的时间. 上方光锥不仅是于同时间点包含了其他空间位置，它也不包含未来时间的x=0，而包含了早先的时间。

当在广义相对论中讨论一系统的演进，或将讨论限定在闵可夫斯基时空，物理学家常提及“光锥”。一个光锥表示一给定现在状态的物体未来任何可能的演进，或给定现在位置之下，未来任何可能的位置。一个物体的未来可能位置受限于该物体能移动的速度，最快只能到光速。举例而言，一个物体于时间位于位置，于时间时，仅能移动到之内的位置。

有些爱因斯坦场方程“局域上”无可异议的精确解含有CTC，其中几个最重要的解包括有：

克尔真空(Kerr vacuum)（不带电荷、磁荷的旋转黑洞模型）

van Stockum尘（具有柱状对称之宇宙尘模型）

哥德尔Λ尘(Gödel lambdadust)（精选宇宙常数项的宇宙尘模形）

提普勒柱体（含有CTC的柱状对称度规）

J. Richard Gott提出了利用宇宙弦制造CTC的机制。

这些例子中的几个如同提普勒柱体，相当复杂而不自然，但克尔解的“外面”部分则被认为某种程度上是一般性的，所以一旦得知其“内部”含有CTC，则令人相当不安。