- 阶梯函数

阶梯函数
概念
一个阶梯函数就是一个分段常值函数,只是含有的阶段很多但是有限。
定义在![]() 上的数值函数
上的数值函数![]() 是阶梯函数,是指对任意的
是阶梯函数,是指对任意的![]() ,存在
,存在![]() 上的一个阶台函数
上的一个阶台函数![]() ,使得对任意的
,使得对任意的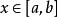 ,有
,有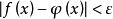 。
。
于是说![]() 被
被![]() 一致地逼近,误差为
一致地逼近,误差为![]() 。这相当于说,所谓
。这相当于说,所谓![]() 是阶梯函数,是指
是阶梯函数,是指![]() 是一致收敛的阶台函数
是一致收敛的阶台函数![]() 的序列的(一致)极限。
的序列的(一致)极限。
如果![]() 是阶梯函数,则
是阶梯函数,则![]() 是有界的。实际上,从对任意的
是有界的。实际上,从对任意的![]() 成立的
成立的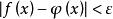 ,得
,得
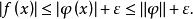
代数性质
性质1:在![]() 上的阶梯函数形成一矢量空间,这空间用
上的阶梯函数形成一矢量空间,这空间用![]() 来表示。
来表示。
这个性质是明显的。例如,从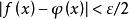 ,
,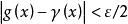 ,得
,得
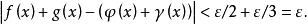
还要指出,![]() 是
是![]() 的子空间。
的子空间。
性质2:如果![]() 是阶梯函数,则
是阶梯函数,则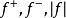 也是阶梯函数。
也是阶梯函数。
只须对![]() 做证明即可;这性质来自
做证明即可;这性质来自
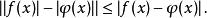
结果是,对两个(或有限多个)阶梯函数![]() ,
,![]() ,函数
,函数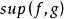 ,
,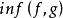 也是阶梯函数。
也是阶梯函数。
性质3:如果![]() 是正阶梯函数或零,则存在一个正阶台函数或;零的序列,一致收敛到
是正阶梯函数或零,则存在一个正阶台函数或;零的序列,一致收敛到![]() 。
。
首先提出,如果对任意的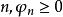 ;又如果
;又如果![]() 收敛到
收敛到![]() ,则
,则![]() 。这是因为对一切
。这是因为对一切![]() ,
,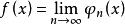 且
且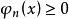 。
。
从上面性质2得到,如果![]() 一致收敛到
一致收敛到![]() ,则同时有
,则同时有![]() 也一致收敛到
也一致收敛到![]() 。可是对一切数值函数有
。可是对一切数值函数有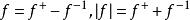 ,由此对
,由此对![]() 使用加法有
使用加法有
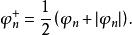
于是![]() 一致收敛到
一致收敛到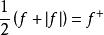 。特别地,如果
。特别地,如果![]() ,则
,则![]() 且
且![]() 是一致收敛到
是一致收敛到![]() 的正阶台函数的序列。[1]
的正阶台函数的序列。[1]

相关百科
-
1641函数信号发生器
2025-11-02 18:06:52 查看详情


 求购
求购










