- 零膨胀模型

零膨胀模型
简介
例如保险索赔次数,索赔数为0的概率很高,否则保险公司就面临破产风险。这种数据数资料中的零值过多,超出了Poisson分布等一般离散分布的预测能力。零膨胀这个概念首先是由Lambert在1992年的论文“Zero-Inflated Poisson Regression,with an Application to Defects in Manufacturing”中提出。
零膨胀泊松
第一个零膨胀模型是Diane Lambert的零膨胀泊松模型,该模型涉及在单位时间内包含过量零计数数据的随机事件。例如,某些类型风险的人口中的保险索赔数量将由那些没有针对风险购买保险而因此无法提出索赔的人实现零膨胀。零膨胀泊松(ZIP)模型采用两个对应于两个零生成过程的组件。第一个过程由生成结构零的二进制分布控制。第二个过程由泊松分布控制,该分布生成计数,其中一些可能为零。两个模型组件描述如下:
![]()
![]()
结果变量![]() 具有任何非负整数值,
具有任何非负整数值,![]() 是
是![]() 个体的预期泊松计数;
个体的预期泊松计数;![]() 是额外零的概率。
是额外零的概率。
平均值为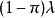 ,方差为
,方差为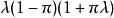 。
。
ZIP的估算
矩估计的方法由下式给出
![]()
![]()
其中![]() 是样本均值,
是样本均值,![]() 是样本方差。
是样本方差。
最大似然估计可以通过求解以下等式找到
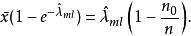 。
。
其中![]() 是样本均值,
是样本均值,![]() 是观察到的零比例。
是观察到的零比例。
这可以通过迭代来解决,并且![]() 的最大似然估计由下式给出:
的最大似然估计由下式给出:
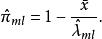 。
。
相关模型
1994年,格林考虑了零膨胀负二项式(ZINB)模型。Daniel B. Hall将Lambert的方法应用于上限计数情况,从而获得零膨胀二项式(ZIB)模型。
离散伪复合泊松模型
如果计数数据![]() 具有零概率的特征大于非零概率,即
具有零概率的特征大于非零概率,即
![]()
那么离散数据![]() 遵循离散伪复合Poisson分布。
遵循离散伪复合Poisson分布。
实际上,让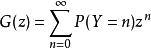 是{\ displaystyle y_ {i}} y_ {i}的概率生成函数。如果
是{\ displaystyle y_ {i}} y_ {i}的概率生成函数。如果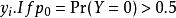 ,则
,则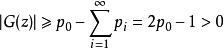 。然后从Wiener-Lévy定理我们证明
。然后从Wiener-Lévy定理我们证明![]() 具有离散伪复合泊松分布的概率生成函数。
具有离散伪复合泊松分布的概率生成函数。
我们说离散随机变量![]() 满足概率生成函数表征
满足概率生成函数表征
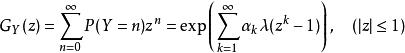
具有参数的离散伪复合泊松分布
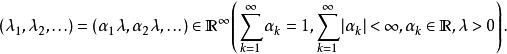
当所有![]() 都是非负数时,它是具有过度离散属性的离散复合泊松分布(非泊松情形)。
都是非负数时,它是具有过度离散属性的离散复合泊松分布(非泊松情形)。

-
Logistic模型
2025-09-19 18:06:04 查看详情 -
气体膨胀式温度传感器
2025-09-19 18:06:04 查看详情


 求购
求购








