- 分母有理化

分母有理化
定义
 分母有理化(3)分母有理化,简称有理化,指的是将该原为无理数的分母化为有理数的过程,也就是将分母中的根号化去。有理化后通常方便运算,有理化的过程可能会影响分子,但分子及分母的比例不变。
分母有理化(3)分母有理化,简称有理化,指的是将该原为无理数的分母化为有理数的过程,也就是将分母中的根号化去。有理化后通常方便运算,有理化的过程可能会影响分子,但分子及分母的比例不变。
单项式
应用一般根号运算:
![]()
![]()
二项式
应用平方差公式:
![]()
![]()
应用立方和、立方差公式:
![]()
![]()
多项式
逐项有理化
![]()
辗转相除法
设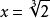 有理化
有理化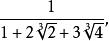
![]()
![]()
![]()
待定系数法
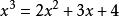 ,求
,求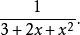
设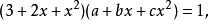
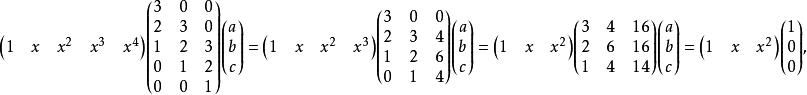
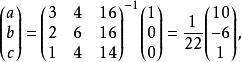
![]()
常规方法
下面介绍两种分母有理化的常规方法,基本思路是把分子和分母都乘以同一个适当的代数式,使分母不含根号[2]。
分母是一个单项式
例如二次根式![]() ,下面将之分母有理化:
,下面将之分母有理化:
![]()
分子分母同时乘以√2,分母变为2,分子变为2√2,约分后,分数值为√2。在这里我们想办法把√2化为有理数,只要变为它的平方即可。
分母是一个多项式
再举一个分母是多项式的例子,如![]() ,下面将之分母有理化:
,下面将之分母有理化:
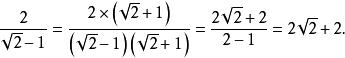
思路仍然是将分子分母同乘相同数。这里使用平方差公式,同时乘上√2+1,分子变为2√2+2,分数值为2√2+2,再约分即可。也就是说,为了有理化多项式的分母,原来分母是减号,我们乘上一个数字相同但用加号连接的式子,再用平方差公式。
此方法可应用到根式大小比较中去。
特殊方法
下面有一些特殊的方法供参考!
分解约简法
将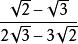 分母有理化:
分母有理化:
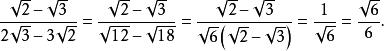
这里我们将分母分解因式后提取出来,这样避免采用平方差公式分解。这种方法较适用于分子分母含有公因式时。
配方约简法
将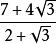 分母有理化:
分母有理化:
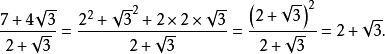
这里我们将分子化成平方式,然后利用完全平方公式配方,再和分母约分,这样避免采用平方差公式分解[3]。
注意事项
下面举一个含参数的二次根式:
将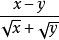 分母有理化:
分母有理化:
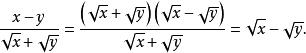
在这里我们将分子用平方差公式分解因式,然后分解!注意在这里我们不能将分母乘以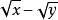 ,因为
,因为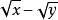 有可能等于0,若分情况讨论又比较麻烦,此时我们就应该注意分子和分母的结构关系[4]!
有可能等于0,若分情况讨论又比较麻烦,此时我们就应该注意分子和分母的结构关系[4]!
拓展
有理化因式
例如:
将分子、分母同时乘以分母的有理化因式。
有理化因式举例
如√a的有理化因式是正负√a,√a+√b的有理化因式是
√a-√b或√b-√a.



 求购
求购









