1. 变上限积分
  1. 首页
  3. 百科
  5. 发动机系统
  7. 变上限积分
变上限积分

变上限积分

中文名 变上限积分
外文名 Cumulativeareafunction
含义 变上限积分的求导及拓展
目录导航

基础定义

变上限积分 是微积分基本 定理之一，通过它可以得到“牛顿——莱布尼茨”定理，它是连接不 定积分和定积分的桥梁，通过它把求定积分转化为求原函数，这样就使数学家从求定积分的和式 极限中解放出来了，从而可以通过原函数来得到积分的值！

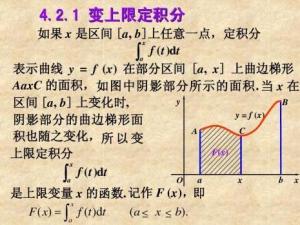变上限积分变上限积分

定义

设函数f(x)在区间[a，b]上可积，如右图：

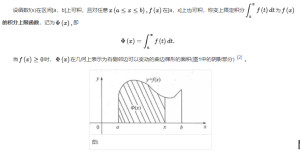定义定义

定理

设函数在区间[a，b]上连续，则积分上限函数

在[a，b]上可导，如右图：

定理定理

相关百科
返回顶部
产品求购 求购