- 简单多面体

简单多面体
定义
一个多面体,如果满足下列条件,就叫做简单多面体:
(1) 各面都是简单多边形;
(2) 多面体的棱彼此之间、棱与面的内部都没有公共点;
(3) 多面体的各顶不附着于各面的内部或各棱之上;
(4) 多面体上共有一顶的一切面角,围拱着这个顶只构成一个多面角。
对于多面体,如果它们经过拓扑变换可变为球面,那么它们都是简单多面体。
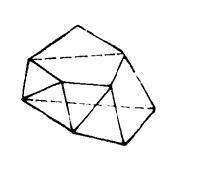 图1
图1
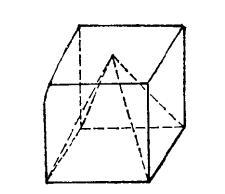 图2
图2
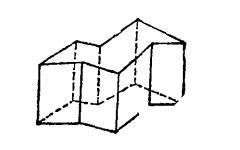 图3
图3
图1是一个简单多面体,图2所示的多面体不是简单多面体,因为它的一个顶点附着在多面体的一个面内。图3所示多面体是由八个矩形和两个凹八边形组成的十面体,它也是个简单多面体。
特别需要指出的是,所有凸多面体都是简单多面体[1]。
欧拉定理
简单多面体的顶点数V,面数F,棱数E,恒有下面的关系式:
![]()
证明:将简单多面体的一个面去掉,设想它是橡皮膜上画着的,这样可以摊在平面上,成一平面图形,这个过程中,顶点数V,棱数E均未改变,只是面数减少1记为F1。因此要证简单多面体有V+F-E = 2,只要对相应的平面网络证V+F1-E =1即可。
(1) 去掉一条棱,除去一个圈,因而减少一个面。顶点数不发生变化。所以V+F1-E的值不变,直到把所有的圈都除掉为止,网络变成一棵树。这时V+F1-E值仍保持不变。
(2) 从所剩的树中去掉一个叶子,就减去一个顶点,减少一条边,此时V+F1-E仍保持不变,到最后只剩下两个顶点一条边,V+F1-E仍保持不变,但此时V= 2,F1=0,E=1,V+F1-E=2+0-1=1。
所以:V+F-E =1+1= 2。
欧拉定理揭示了简单多面体的顶点数、面数、棱数存在着的关系:V+F-E = 2。常数2是简单多面体经过拓扑变换下的不变数。它是一个与通常的长度、角度、面积、体积等度量无关的数。
欧拉定理(或欧拉公式)是拓扑学中的一个重要公式,在初等几何中对于讨论凸多面体的顶数、棱数、面数的有关命题十分重要。
为了便于叙述,我们把简单多面体的顶点数、面数、棱数分别记为V、F、E,其三面角、四面角、五面角...的顶点数依次记为V3,V4,V5,...其面上的三角形、四边形、五边形...的面数,依次记为F3,F4,F5,...。
显然有:
命题1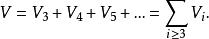
命题2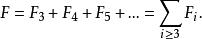
命题3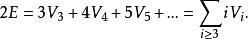
证明:由于![]() 为i 面角的顶数,
为i 面角的顶数,![]() 为从各个i 面角的顶点发出的棱数之和,而
为从各个i 面角的顶点发出的棱数之和,而![]() 为从各个顶点发出的棱数的总和,在
为从各个顶点发出的棱数的总和,在![]() 中,每条棱均从两个顶点发出,因而每条棱都被计算了两次,则
中,每条棱均从两个顶点发出,因而每条棱都被计算了两次,则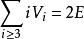 。
。
命题4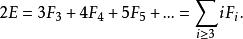
命题5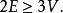
命题6设一个简单多面体的多面角都是三面角,则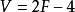 。
。
命题7在凸面体中,有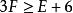 。
。
定理空间仅存五种正多面体[1]。
多面体的有关知识
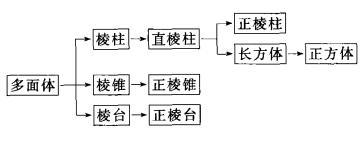 图4
图4
1. 简单多面体的基础知识包括棱柱、棱锥的概念、性质、侧面积、表面积、截面积、体积的计算。简单旋转体的基础知识包括圆柱、圆锥、球的表面积、体积计算。简单多面体的分类,正多面体的性质等知识。
2. 以柱、锥和特殊简单多面体为载体的立体几何综合型问题研究既要运用线面关系的判定定理、性质定理,又要运用其基本性质。
3. 简单几何体面积与体积计算。侧面积和体积的计算首先要熟记公式,并能用函数的观点去理解柱、锥、球的面积公式和体积公式,理解其变化规律[2]。
多面体的有关概念
(1)多面体:由若干个平面多边形围成的空间图形叫做多面体。
(2)凸多面体:把一个多面体的任何一个面伸展成平面,如果其余各面都位于这个平面的同一侧,这样的多面体叫做凸多面体。
(3)正多面体:每个面都是有相同边数的正多边形,以每个顶点为端点都有相同棱数的凸多面体,叫做正多面体,正多面体只有五种。
(4)简单多面体:表面经过连续变形可变为球面的多面体,叫做简单多面体,如棱柱、棱锥、正多面体等[3]。

-
奥迪tfsi是什么意思的简单介绍
2025-09-28 04:26:38 查看详情 -
为什么汽车油表不准,油表不准简单解决办法
2025-09-28 04:26:38 查看详情 -
如何估价汽车价格 最简单的二手车估价方法
2025-09-28 04:26:38 查看详情 -
二手汽车价格如何估算 最简单的二手车估价方法
2025-09-28 04:26:38 查看详情 -
大众朗逸怎么样 朗逸怎么样给大家简单的介绍一下
2025-09-28 04:26:38 查看详情


 求购
求购





