- 第一型曲面积分

第一型曲面积分
中文名
第一型曲面积分
相关书籍
数学分析
定义
设![]() 为空间中的曲面,
为空间中的曲面,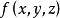 为定义在
为定义在![]() 上的函数.对曲面
上的函数.对曲面![]() 作分割
作分割![]() ,它把分成
,它把分成![]() 个可求面积的小曲面片
个可求面积的小曲面片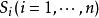 ,
,![]() 的面积记为
的面积记为![]() ,分割
,分割![]() 的细度为
的细度为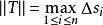 ,在
,在![]() 上任取一点
上任取一点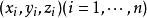 , 若存在极限
, 若存在极限
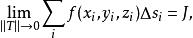 且它的值与分割及点的取法无关,则称此极限
且它的值与分割及点的取法无关,则称此极限![]() 为
为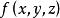 在
在![]() 上的第一型曲线积分[1],记为
上的第一型曲线积分[1],记为
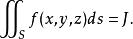 或者简写成
或者简写成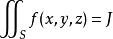 。
。
计算
设空间曲面S的方程为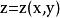 ,
,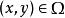 ,其中
,其中![]() 为曲面S在
为曲面S在![]() 平面上的投影域,函数
平面上的投影域,函数![]() 在曲面S上连续,如果
在曲面S上连续,如果![]() 在
在![]() 上有连续的一阶偏导数,则有
上有连续的一阶偏导数,则有
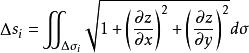
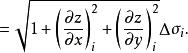
其中![]() 是
是![]() 在
在![]() 上的投影域,
上的投影域,![]() 和
和![]() 表示在
表示在![]() 内某点
内某点![]() 处的两个偏导数。由第一型曲面积分的定义,于是将第一型曲面积分化为二重积分的计算[1]
处的两个偏导数。由第一型曲面积分的定义,于是将第一型曲面积分化为二重积分的计算[1]
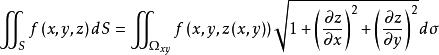
物理意义
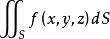 表示以
表示以 为面密度的空间曲面S的“质量”,即将空间曲面S想象成一块光滑的(可微的)不折叠的(单值的)质量分布服从
为面密度的空间曲面S的“质量”,即将空间曲面S想象成一块光滑的(可微的)不折叠的(单值的)质量分布服从 的薄板,故
的薄板,故 在S上的第一型曲面积分就是薄板的代数质量[2]。
在S上的第一型曲面积分就是薄板的代数质量[2]。
性质
第一型曲面积分具有下述一些重要性质[1]:
1).若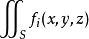 存在,
存在,![]() 为常数,则
为常数,则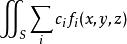 也存在,且
也存在,且
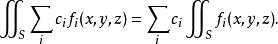
2).若曲面![]() 由互不相交的曲面块
由互不相交的曲面块 组成,且
组成,且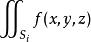 都存在,则
都存在,则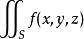 也存在,且
也存在,且
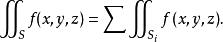
3).若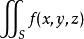 与
与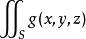 都存在,且在
都存在,且在![]() 上
上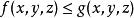 , 则
, 则
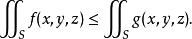
4).若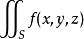 存在,则
存在,则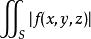 也存在,且
也存在,且

应用
下面给出二个常用的应用。
1)空间曲面S的重心坐标为[2]
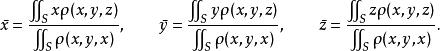
2)曲面S绕z轴(x, y轴)的转动惯量是[2]
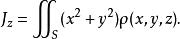
其中![]() 为曲面的密度函数。
为曲面的密度函数。

相关百科
-
新款斯巴鲁BRZ上市 雪佛兰开拓者将推5款车型
2025-10-29 22:29:50 查看详情 -
全新紧凑型SUV/上半年上市 别克昂科拉PLUS最新谍照
2025-10-29 22:29:50 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-10-29 22:29:50 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-10-29 22:29:50 查看详情 -
将于1月6日上市 450六座版车型上市
2025-10-29 22:29:50 查看详情 -
捷途X95热爱Pro版上市 别克微蓝6插混车型上市
2025-10-29 22:29:50 查看详情 -
欧拉闪电猫将于10月31日上市 新增1.5T车型
2025-10-29 22:29:50 查看详情 -
25T车型上市 预售价17.77
2025-10-29 22:29:50 查看详情 -
凯迪拉克CT6新车型上市 W帅气亮相
2025-10-29 22:29:50 查看详情 -
POWER版车型上市 油耗1.7L/100km
2025-10-29 22:29:50 查看详情


 求购
求购

