非奇异线性变换

定义1.1 设V是域P上的线性空间，σ∈HomP(V，V)，若存在λ∈HomP(V，V)，使λσ=E(单位线性变换)，则称σ为非奇异线性变换；否则，称为奇异线性变换。^[1]

注：当dim V=n时，非奇异线性变换亦称为非退化线性变换，或满秩线性变换，或正则线性变换。在dim V=n的条件下，σ是可逆的充分必要条件为σ是非奇异的，因此，在有限维的条件下也可以说非奇异线性变换就是可逆线性变换。^[1]

定义1.2 设x1，x2，...，xn；y1，y2，...，yn是两组文字，系数在数域P中的一组关系式：

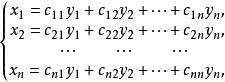称为由x1，x2，...，xn到y1，y2，...，yn的一个线性替换，或简称线性替换。如果系数行列式

那么上述线性替换就称为非退化的。^[2]

例如^[2]，在解析几何中，我们看到，当坐标原点与中心重合，一个有心二次曲线的一般方程是

为了便于研究这个二次曲线的几何性质，我们可以选择适当的角度θ，作转轴（反时针方向转轴）

把方程化成标准方程。

如果把

看成线性替换，那么它就是非退化的，因为

1.^[2]因为二次型和它的矩阵是相互唯一决定的，令

故线性替换

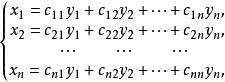可以写成

2.^[2]经过一个非退化的线性替换，二次型还是变成二次型。具体地：设

是一个二次型，作非退化线性替换

我们可以得到一个的二次型

故有

容易看出，矩阵

也是对称的，这就是前后两个二次型的关系。

3.^[2]经过非退化的线性替换，新二次型的矩阵与原二次型的矩阵是合同的。