切比雪夫多项式

第一类切比雪夫多项式由以下递推关系确定

也可以用母函数表示

第二类切比雪夫多项式由以下递推关系给出

此时母函数为

第一类切比雪夫多项式由以下三角恒等式确定

其中 n = 0, 1, 2, 3, .... . 是关于 的 n次多项式，这个事实可以这么看： 是:的实部（参见棣莫弗公式），而从左边二项展开式可以看出实部中出现含的项中，都是偶数次的，从而可以表示成 的幂 。

用显式来表示

尽管能经常碰到上面的表达式，但如果借助于复函数cos(z), cosh(z)以及他们的反函数，则有

类似，第二类切比雪夫多项式满足

切比雪夫多项式可被定义为佩尔方程

在多项式环R[x] 上的解(e.g., 见 , p.70). 因此它们的表达式可通过解佩尔方程而得出:

两类切比雪夫多项式可由以下双重递归关系式中直接得出:

证明的方式是在下列三角关系式中用 代替

T_n 和U_n 都是区间[−1,1] 上的正交多项式系.

第一类切比雪夫多项式带权

即:

可先令x= cos(θ) 利用T_n (cos(θ))=cos(nθ)便可证明.

类似地，第二类切比雪夫多项式带权

即:

其正交化后形成的随机变量是 Wigner 半圆分布).

对每个非负整数， 和 都为 次多项式。 并且当为偶（奇）数时，它们是关于 的偶（奇）函数， 在写成关于的多项式时只有偶（奇）次项。

时， 的最高次项系数为 ，时系数为 。

对，在所有最高次项系数为1的次多项式中 ， 对零的偏差最小，即它是使得在 上绝对值的最大值最小的多项式。 其绝对值的最大值为 ， 分别在 、 及 的其他 个极值点上达到 。

两类切比雪夫多项式间还有如下关系：

切比雪夫多项式是超球多项式或盖根堡多项式的特例, 后者是雅可比多项式的特例.

切比雪夫多项式导数形式的递推关系可以由下面的关系式推出：

<1¼, -1¼<1¼; 按颜色依次是T₀, T₁, T₂, T₃, T₄ T₅." titlename="前六个第一类切比雪夫多项式的图像，其中-1¼<1¼, -1¼<1¼; 按颜色依次是T₀, T₁, T₂, T₃, T₄ T₅."/>

前几个第一类切比雪夫多项式是

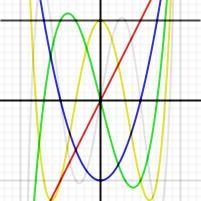<1¼, -1¼<1¼; 按颜色依次是U₀, U₁, U₂, U₃, U₄ U₅. 虽然图像中无法显示,我们实际有 U_n(1)=n+1 以及 U_n(-1)=(n+1)(-1)ⁿ." titlename="前六个第二类切比雪夫多项式的图像，其中-1¼<1¼, -1¼<1¼; 按颜色依次是U₀, U₁, U₂, U₃, U₄ U₅. 虽然图像中无法显示,我们实际有 U_n(1)=n+1 以及 U_n(-1)=(n+1)(-1)ⁿ."/>

前几个第二类切比雪夫多项式是

第一类切比雪夫多项式前几阶导数是

一个N 次多项式按切比雪夫多项式的展开式为如下：

多项式按切比雪夫多项式的展开可以用 Clenshaw递推公式计算。

两类的n次切比雪夫多项式在区间[−1,1]上都有n 个不同的根, 称为切比雪夫根, 有时亦称做 切比雪夫节点 ，因为是多项式插值时的 插值点 . 从三角形式中可看出T_n 的n个根分别是：

类似地， U_n 的n个根分别是：