- 非线性积分方程

非线性积分方程
基本介绍
不具有线性性质的一类积分方程就是非线性积分方程。如果未知函数在积分号下是以非线性形式出现的,这种方程就称为非线性积分方程。例如,
![]() 当
当![]() 不是
不是![]() 的线性函数时,就是非线性积分方程。非线性积分方程也可以被分成多种类型,例如,弗雷德霍姆型、沃尔泰拉型、哈默斯坦型等。
的线性函数时,就是非线性积分方程。非线性积分方程也可以被分成多种类型,例如,弗雷德霍姆型、沃尔泰拉型、哈默斯坦型等。
由于自然界和工程技术中出现的大量问题都是非线性的,因此,在数学物理中研究过的一些线性方程,只能是在一定条件下对实际问题的近似描述。为了更精确地刻画客观现象,就完全有必要研究非线性积分方程。如果把积分方程中出现的函数看做是巴拿赫空间X中的元素,把原来的积分运算用算子T来代替,就将得到一个算子方程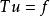 。
。
近年来非线性积分方程的研究已有很大的发展,但是还没有系统的理论。即使是讨论可解性问题上也存在着不少困难,这主要是与线性积分方程的研究方法有着本质的不同。这一理论的进一步发展在很大程度上依赖于现代泛函分析、算子理论以及绍德尔不动点原理等数学分支的发展[1]。
Fredholm型非线性积分方程
考虑下列Fredholm(弗雷德霍姆)型非线性积分方程
![]() 其中
其中![]() 是参数,
是参数,![]() 是变量
是变量 的未知函数。
的未知函数。
定理1设![]() 是
是![]() 上的实连续函数,
上的实连续函数,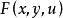 是
是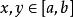 和
和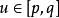 的连续函数,关于u满足Lipschitz条件:
的连续函数,关于u满足Lipschitz条件:
![]() 其中
其中![]() 及
及![]() 均为常数,此时存在常数,
均为常数,此时存在常数,![]() 及
及![]() ,使
,使 ,及
,及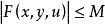 ,不妨设
,不妨设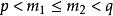 ,则当参数
,则当参数![]() 适合条件
适合条件
![]()
时,方程(1)有惟一连续解,这个解可用逐次逼近法求出:
![]()
![]() 并且函数列
并且函数列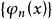 绝对一致收敛到方程(1)的解[2]。
绝对一致收敛到方程(1)的解[2]。
Volterra型非线性积分方程
考虑如下Volterra(沃尔泰拉)型非线性积分方程:
![]()
定理2设![]() 是定义在
是定义在![]() 上的已知实连续函数,
上的已知实连续函数,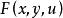 是
是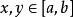 和
和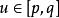 的连续函数,且关于u满足Lipschitz条件。这里
的连续函数,且关于u满足Lipschitz条件。这里![]() 为常数,则存在常数
为常数,则存在常数![]() 及
及![]() ,使
,使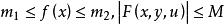 ,不妨设
,不妨设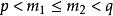 ,则当
,则当![]() 满足条件
满足条件
![]() 时,方程(2)有惟一连续解。可由如下迭代得到
时,方程(2)有惟一连续解。可由如下迭代得到
![]()
![]() 且
且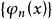 绝对一致收敛到(2)的解[2]。
绝对一致收敛到(2)的解[2]。
Hammertein型非线性积分方程
在非线性积分方程中,研究较多的是下列的Hammerstein(哈默斯坦)型积分方程(integral equation of the Hammerstein type)。
![]() 其中
其中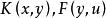 为已知函数。
为已知函数。
定理1设核![]() 是连续实对称正核,
是连续实对称正核,![]() 连续并满足如下条件:
连续并满足如下条件:
(1) 存在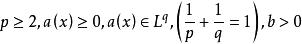 ,使得
,使得
![]()
(2) 存在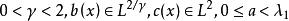 ,使得
,使得
![]() 其中
其中![]() 真是积分算子
真是积分算子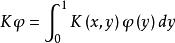 的最小特征值,则方程(3)在
的最小特征值,则方程(3)在![]() 中至少有一解。
中至少有一解。
定理2设核![]() 为连续实对称正核,
为连续实对称正核,![]() 连续,并且存在
连续,并且存在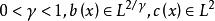 及
及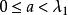 (
(![]() 同上),使
同上),使
![]() 则(3)在
则(3)在![]() 中至少有一解。
中至少有一解。
定理3如果对任何固定的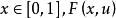 是u的非减函数,则(3)至多有一解[2]。
是u的非减函数,则(3)至多有一解[2]。

-
非线性方程组数值解法
2025-09-29 02:22:05 查看详情 -
比例积分电动三通调节阀
2025-09-29 02:22:05 查看详情 -
非线性阈值协整理论及其在中国的应用研究
2025-09-29 02:22:05 查看详情 -
加油卡怎么使用(邮政积分兑换加油卡怎么使用)
2025-09-29 02:22:05 查看详情


 求购
求购









