1. 规范正交系
  1. 首页
  3. 百科
  5. 发动机系统
  7. 规范正交系

规范正交系

中文名 规范正交系
范畴 正交系
领域 数学
目录导航

简介

设M是内积空间X的一个不含零子集，若M中向量两两正交，则称M为X中的正交系，又若M中向量的范数都为1，则称M为X中的规范正交系。

元素的正交性在内积空间和Hilbert空间中扮演着十分重要的角色。在n维欧氏空间，选定n个相互正交的向量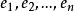，则形成n维空间中的一组正交基，也就是说在空间中建立了一组坐标系，空间中的任何一个元素都可以由这组坐标的线性组合表示出来。

其中。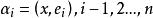

Rn为n维欧氏空间，则向量集

为Rn中规范正交系，其中

基本性质

（1）对正交系M中任意有限个向量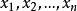，有

事实上，由于M中向量两两正交，所以

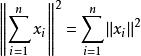
（2）正交系M是X中线性无关子集。

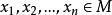事实上，设，而且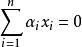，其中为n个数，则对任何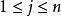，有

由于，因此，所以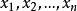线性无关，从而说明M是X中线性无关子集。

应用

在傅里叶系数

设M为内积空间X中的规范正交系，，称数集

为向量x关于规范正交系M的傅里叶系数集。

而称为x关于e傅里叶系数。

在Bessel不等式

设是内积空间中的有限或可数规范正交系，则对，有

在级数

设是Hilbert空间中的可数规范正交系，则

（1）级数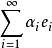收敛的充要条件为级数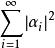收敛。

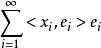（2）对，级数收敛。

举例

在空间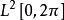中，定义内积为

则三角函数系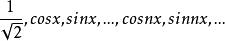为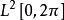中规范正交系，所以内积空间中规范正交系是正交函数系概念的推广。

相关百科
返回顶部
产品求购 求购