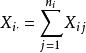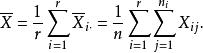- 偏差平方和

偏差平方和
基本介绍
在单因素实验中,为了使造成各随机变量之间的差异的大小能定量表示出来,引入:
记在水平下样本和为,其样本均值为因素A下的所有水平的样本总均值为
为了通过分析对比产生样本
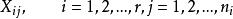 之间差异性的原因,从而确定因素A的影响是否显著,我们引人偏差平方和来度量各个体间的差异程度
之间差异性的原因,从而确定因素A的影响是否显著,我们引人偏差平方和来度量各个体间的差异程度
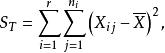 因
因![]() 能反映全部试验数据之间的差异,所以又称为总偏差平方和[2]。
能反映全部试验数据之间的差异,所以又称为总偏差平方和[2]。
偏差平方和的分解
如果![]() 成立,则r个总体间无显著差异,也就是说因素A对指标没有显著影响,所有的
成立,则r个总体间无显著差异,也就是说因素A对指标没有显著影响,所有的![]() 可以认为来自同一个总体
可以认为来自同一个总体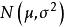 ,各个
,各个![]() 间的差异只是由随机因素引起的,若
间的差异只是由随机因素引起的,若![]() 不成立,则在总偏差中,除随机因素引起的差异外,还包括由因素A的不同水平的作用而产生的差异,如果不同水平作用产生的差异比随机因素引起的差异大得多,就认为因素A对指标有显著影响,否则,认为无显著影响。为此,可将总偏差中的这两种差异分开,然后进行比较。
不成立,则在总偏差中,除随机因素引起的差异外,还包括由因素A的不同水平的作用而产生的差异,如果不同水平作用产生的差异比随机因素引起的差异大得多,就认为因素A对指标有显著影响,否则,认为无显著影响。为此,可将总偏差中的这两种差异分开,然后进行比较。
记
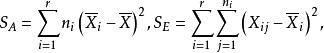 则有下面的定理:
则有下面的定理:
定理1(平方和分解定理)令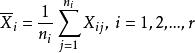 ,有
,有

![]() 表示在水平
表示在水平![]() 下样本值与样本均值之间的差异,它是由随机误差引起的,称为误差平方和或组内平方和。
下样本值与样本均值之间的差异,它是由随机误差引起的,称为误差平方和或组内平方和。![]() 反映在每个水平下的样本均值与样本总均值的差异,它是由因素A取不同水平引起的,称为因素A的效应平方和或组间平方和,
反映在每个水平下的样本均值与样本总均值的差异,它是由因素A取不同水平引起的,称为因素A的效应平方和或组间平方和, 式就是我们所需要的平方和分解式[2]。
式就是我们所需要的平方和分解式[2]。
SE与SA的统计特性
如果![]() 成立,则所有的
成立,则所有的![]() 都服从正态分布
都服从正态分布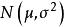 ,且相互独立,则有:
,且相互独立,则有:
定理2
(1)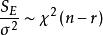 ,且
,且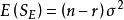 ,所以
,所以![]() 为
为![]() 的无偏估计;
的无偏估计;
(2) ,且
,且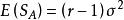 ,因此
,因此![]() 为
为![]() 的无偏估计;
的无偏估计;
(3)![]() 与
与![]() 相互独立;
相互独立;
(4)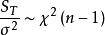 。
。

相关百科


 求购
求购