质量函数

注意这在所有实数上，包括那些X不可能等于的实数值上，都定义了 fX(x)。在那些X不可能等于的实数值上， fX(x)取值为0 ( x ∈ R\S，取Pr(X = x) 为0)。

离散随机变量概率质量函数的不连续性决定了其累积分布函数也不连续。

例子

假设X是抛硬币的结果，反面取值为0，正面取值为1。则在状态空间{0, 1}(这是一个Bernoulli随机变量)中，X = x的概率是0.5，所以概率质量函数是：

公式图片

概率质量函数可以定义在任何离散随机变量上，包括常数分布, 二项分布 (包括Bernoulli分布), 反二项分布, Poisson分布, 几何分布以及超几何分布随机变量上.

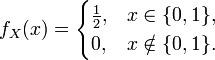取自"http://zh.wikipedia.org/w/index.php?title=%E6%A6%82%E7%8E%87%E8%B4%A8%E9%87%8F%E5%87%BD%E6%95%B0&variant=zh-cn"

维基百科，自由的百科全书

初始质量函数（缩写为IMF）是同一个星族中单位体积内新形成的恒星的相对数目在质量上的分布，是恒星形成中的一个重要概念。初始质量函数首先是由萨尔彼得在1955年引入的[1]，他将大于1倍太阳质量的初始质量函数写为

ξ(M) = ξ0M − 2.35

其中M是恒星质量，ξ(M)是单位质量内新形成的恒星的数目，上式也称为萨尔彼得方程。1979年Glenn E. Miller和John M. Scalo给出了1倍太阳质量以下的初始质量函数[2]，称为Miller-Scalo初始质量函数。

参考文献

^ Salpeter, E.E., 1955, Astrophysical Journal, 121, 161. NASA ADS

^ Miller, G. E., Scalo, J. M., 1979, Astrophysical Journal Supplement Series, 41, 513. DOI:10.1086/190629 NASA ADS