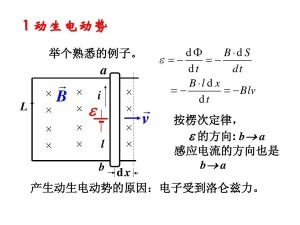
- 动生电动势

动生电动势
简介
 动生电动势假设,电荷Q移动经过一个电动势源后,获得了能量W,则此元件的电动势定义为
动生电动势假设,电荷Q移动经过一个电动势源后,获得了能量W,则此元件的电动势定义为![]() 。通常,这能量是分离正负电荷所做的功,由于这正负电荷被分离至元件的两端,会出现对应电场与电压差。
。通常,这能量是分离正负电荷所做的功,由于这正负电荷被分离至元件的两端,会出现对应电场与电压差。
在电磁学里,电动势又分为两种:“感生电动势”与“动生电动势”。根据法拉第感应定律,处于含时磁场的闭电路,由于磁场随着时间而改变,会有感生电动势出现于闭电路。感生电动势等于电场沿着闭电路的路径积分。处于闭电路的带电粒子会感受到电场,因而产生电流。
移动于磁场的细直导线,其内部会出现动生电动势。处于这导线的电荷,根据洛伦兹力定律,会感受到洛伦兹力,从而造成正负电荷分离至直棍的两端。这动作会形成一个电场与伴随的电场力,抗拒洛伦兹力,直到两种作用力达成平衡。
设回路正方向为顺时针,
通过回路磁通量为: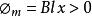
动生电动势为:
![]()
负号表明动生电动势方向是反时针。[3]
历史
从1825年到1826年之间,格奥尔格·欧姆做了很多有关于电路的实验。1827年,在他发表的书《直流电路的数学研究》(Die galvanische Kette, mathematisch bearbeitet)里面,论述了很多这些实验和从这些实验中得到的结果,包括著名的“欧姆定律”。欧姆注意到电路所需要的电源是由电池供给的,电池与电路内的各种物理现象应该有密切关系。他推论电池具有某种“驱动力”,能够驱使电流流动于电路。他将几个伏打电池串联在一起,发觉电流与伏打电池的数量成正比。因此,他提出驱动力与电流成正比。这驱动力就是我们所知的电动势,在一个简单的电阻电路里,电动势等于电流乘以电阻。
 动生电动势后来,于1831年,麦可·法拉第做了一系列有关电磁感应的实验,从这些实验,他发现以下几点:
动生电动势后来,于1831年,麦可·法拉第做了一系列有关电磁感应的实验,从这些实验,他发现以下几点:
- 当改变载流导线的电流时,附近的闭电路会被感应出电流。
- 当移动磁铁时,附近的闭电路会被感应出电流。
- 当移动闭电路于载流导线或磁铁附近时,这闭电路会被感应出电流。
于1832年,法拉第又发现,产生于不同导线的感应电流与导线的电导率成正比。由于电导率与电阻成反比,这显示出感应作用涉及了电动势,感应电流是由电动势驱使导线的电荷移动而形成的;而且,不论导线是开电路,或是闭电路,都会感应出电动势。[4]
性质
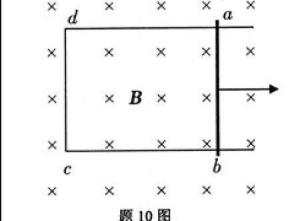
动生电动势的非静电力;
动生电动势的非静电力是洛仑兹力!
导体内电子受洛仑兹力为:
![]()
洛仑兹力克服静电场力,将电子从高电位移向低电位作功,使导体ab两端形成电势差,产生电动势。
论证
动生电动势来源于磁场对运动导体中带电粒子的洛伦兹力。由洛伦兹力公式 F=qvB,当导体中的带电粒子在恒定磁场B中以速度v运动时,F'=evB,单位正电荷所受洛伦兹力为evB。此洛伦兹力与引起动生电动势的非静电力有关,但此洛伦兹力并不是非静电力。根据电动势的定义,非静电力将电子从正极搬到负极做功为E=BvL,上述洛伦兹力并不参与做功。
可以证明,上述积分等于回路在磁场中运动时,磁通量变化率的负值。即与法拉第电磁感应定律一致。
感应电动势分类
第一类:动生电动势:
磁场恒定,导体或回路运动→![]() 动。
动。
第二类:感生电动势:
![]() 磁场随时间变化,导体或回路静止→感。
磁场随时间变化,导体或回路静止→感。
动生电动势的计算方法
根据电动势的定义,得导线L的动生电动势为:
![]()
θ是v和B的夹角,φ是dl和v×B的夹角。
动生电动势方向的确定:
动生电动势方向: 朝向非静电场方向,由右手定则确定。
求解动生电动势的方法:
1、确定载流导线的磁场大小和方向;
2、求导线中的动生电动势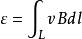 ;
;
3、由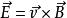 确定动生电动势方向。[5]
确定动生电动势方向。[5]

-
别克纯电动SUV微蓝7将于7月上市 售价13.59
2025-10-31 10:41:47 查看详情 -
EV上市 旗下首款纯电动车型
2025-10-31 10:41:47 查看详情 -
五菱荣光电动车将4月中下旬上市 将于4月底上市
2025-10-31 10:41:47 查看详情 -
五菱荣光电动车将4月中下旬上市 起亚焕驰新增车型上市
2025-10-31 10:41:47 查看详情 -
五菱荣光电动车将4月中下旬上市 博越PRO智能四驱版正式上市
2025-10-31 10:41:47 查看详情 -
五菱荣光电动车将4月中下旬上市 定位中型SUV
2025-10-31 10:41:47 查看详情 -
前脸更像7系/或将于中上市 旗下首款纯电动车型
2025-10-31 10:41:47 查看详情 -
新款领克05正式上市 旗下首款纯电动车型
2025-10-31 10:41:47 查看详情 -
五菱荣光电动车将4月中下旬上市 售价33.89万
2025-10-31 10:41:47 查看详情 -
五菱荣光电动车将4月中下旬上市 东风标致408X正式下线
2025-10-31 10:41:47 查看详情


 求购
求购

