正态性检验

利用观测数据判断总体是否服从正态分布的检验称为正态性检验，它是统计判决中重要的一种特殊的拟合优度假设检验。常用的正态性检验方法有正态概率纸法、夏皮罗维尔克检验法(Shapiro-Wilktest)，科尔莫戈罗夫检验法，偏度-峰度检验法等。

正态性检验问题为

: 总体服从正态分布: 总体不服从正态分布。

在正态性检验中，偏度峰度正态性检验统计量原理清晰、计算

简单，通常被首选用来作为正态性检验统计量。

设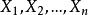。表示来自总体的样本，表示样本均值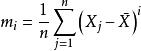，表示 i 阶样本中心矩。正态分布的偏度和峰度均为 0，其中偏度和峰度的定义分别为

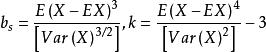
该检验就是根据这个特点来检验分布正态性的。

偏度-峰度正态性检验包括下面三种方法:

偏度检验

使用偏度检验时，总体具有仅在偏度方向上偏离正态的先验信息。因而备择假设为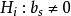。检验统计量为。

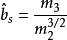当总体服从正态分布时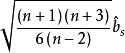，的极限分布是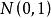，因此水平为 α检验的拒绝域为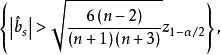这里是标准正态分布的分位数。

峰度检验

使用峰度检验时，总体具有仅在峰度方向上偏离正态的先验信息。因而备择假设为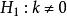。检验的统计量为

。

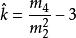当总体服从正态分布时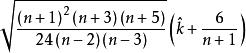的极限分布是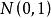，因此水平为α检验的拒绝域为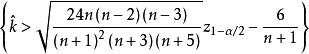或。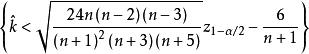

偏度和峰度联合检验

使用联合检验的条件为: 总体具有在偏度和峰度方向上都偏离正态的先验信息，它的备择假设为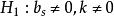。首先计算统计量

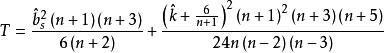
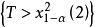的值，然后根据该统计量的极限分布自由度是2 的分布，所以水平为 α检验的拒绝域是，其中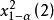是自由度是2的分布的分位数。

考虑变量X 带有测量误差模型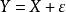的正态性检验问题，服从正态分布不服从正态分布，其中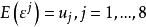已知。

设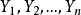是来自上述模型的一组样本，则给出变量X 的偏度-峰度正态性检验统计量的定义如下:

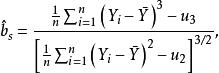
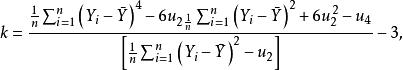
这里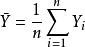。变量 X 的标准化偏度和峰度检验统计量分别定义为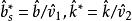：，其中

≥ 24，

偏度检验

使用偏度检验时，总体具有仅在偏度方向上偏离正态的先验信息。因而备择假设为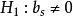。检验统计量为。当总体服从正态分布时，的极限分布是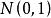,因此水平为检验的拒绝域为。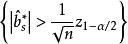

峰度检验

使用峰度检验时，总体具有仅在峰度方向上偏离正态的先验信息。因而备择假设为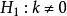。检验的统计量为当总体服从正态分布时,的极限分布是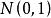，因此水平为检验的拒绝域为。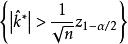

偏度和峰度联合检验

使用联合检验的条件为: 总体具有在偏度和峰度方向上都偏离正态的先验信息，它的备择假设为: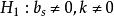，首先计算统计量

的值，然后根据该统计量的极限分布自由度是 2 的分布，所以拒绝域是。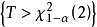

在一定的条件下，这些偏度和峰度检验统计量具有渐近正态的优良性质和良好的功效。

图形中的垂直尺度类似于正态概率图中的垂直尺度。水平轴为线性尺度。此线形成数据所来自总体的累积分布函数的估计值。图中会显示总体参数的数字估计（Xbar和 s）、正态性检验值以及关联的p 值。^[1]