卡尔达诺公式

卡尔达诺公式是一个著名的求根公式，指实系数一元三次方程

的求根公式x=α+β，式中

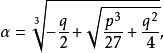
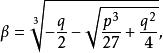且αβ=-p/3，此公式也可以应用于复系数三次方程中^[2]。

意大利数学家卡尔达诺(G.Cardano)在1545年出版的《大术》一书中，首先发表了上述公式，此公式来自意大利数学家塔尔塔利亚(N.Tartaglia)，但卡尔达诺给出了该公式的几何证明。

当p，q为实数时，称

为方程(1)的判别式。

当D>0时，方程(1)有三个两两不同的实根，称为不可约情形；

当D=0时，方程(1)有三个实根，当p，q均不为0时，有两个重根和一个单根；

当D<0时，方程(1)有一个实根与两个共轭虚根^[2]。

卡尔达诺公式表明三次方程有根式解，他的学生费拉里(L.Ferrari)用降阶法获得一元四次方程的根式解法，从而引发了人们对五次以上代数方程的根式解的研究，推动了近世代数学的产生和发展.此外，由于在不可约情形中出现了用虚数表示实根的情形，使人们再次遇到负数开平方，因此促进了对虚数合理性的认识.1572年，意大利数学家邦贝利(Bombelli，R.)在他的《代数》一书中，讨论过求解一元三次方程x3=15x+4，其三个根为4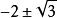，。但应用卡尔达诺公式却是

邦贝利研究后认为，应将负数的平方根像“普通数”那样运算.后来，德国数学家莱布尼茨(Leibniz，G.W.)也研究过不可约情形，并且深信：用代数方法解此种情形不可能不用到虚数.这使人们逐渐认识到负数开平方有一定的客观基础和合理性，加快了人们接受虚数的认识进程.法国数学家韦达(F.Viete)在《论方程的识别与订正》(完成于1591年，出版于1615年)中，利用三角恒等式给出了不可约情形的方程(1)的根为

式中θ满足

韦达只给出其中一个根。

利用卡尔达诺公式还会出现用无理数表示有理根的情形。例如，方程x3-x-6=0有一个根2，但用卡尔达诺公式却为

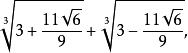因此，在实际求根时，卡尔达诺公式有一定的局限性^[2]。