斜渐近线

若当x趋向于无穷时，函数y=f(x)无限接近一条固定直线y=Ax+B（函数y=f(x)与直线y=Ax+B的垂直距离PN无限小，且limPN=0），当然也即PM=f(x)-(Ax+B)的极限为零，则称y=Ax+B为函数y=f(x)的斜渐近线。

分析(在x趋向无穷时)

斜渐近线的正确求法(在x趋向于无穷时)

；

所以f(x)的斜渐近线方程为

y=Ax+B

斜渐近线

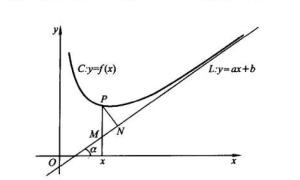
如图所示，

直线y=Ax+B与x轴正向夹角为α，则有

PN=PM·cosα=[f(x)-(Ax+B)]cosα .

按照斜渐近线定义，我们知道有limPN=0，而cosα是常数，所以

lim[f(x)-(Ax+B)]=0.

所以可得:

A=lim[f(x)/x]，B=lim[f(x)-ax] .

反之，亦然，证毕。

当a=0时，有limf(x)=b (x趋向于无穷时)，此时称y=b为函数f(x)的水平渐近线。所以，水平渐近线只是斜渐近线的一种特殊情况。解题时，我们可以不考虑水平渐近线，而只考虑斜渐近线和铅直渐近线。