- 三角形中位线

三角形中位线
定理
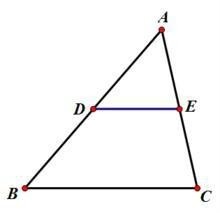
 三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半
三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半
三角形的中位线
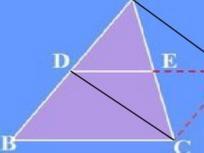
证明 如图,已知△ABC中,D,E分别是AB,AC两边中点。
求证DE平行且等于BC/2
法一:过C作AB的平行线交DE的延长线于F点。
∵CF∥AD
∴∠A=∠ACF
∵AE=CE、∠AED=∠CEF
∴△ADE≌△CFE
∴AD=CF
∵D为AB中点
∴AD=BD
∴BD=CF
∴BCFD是平行四边形
∴DF∥BC且DF=BC
∴DE=BC/2
∴三角形的中位线定理成立.
法二:利用相似证
∵D,E分别是AB,AC两边中点
∴AD=AB/2 AE=AC/2
∴AD/AE=AB/AC
又∵∠A=∠A
∴△ADE∽△ABC
∴DE/BC=AD/AB=1/2
∴∠ADE=∠ABC
∴DF∥BC且DE=BC/2
法三:坐标法:
设三角形三点分别为(x1,y1),(x2,y2),(x3,y3)
则一条边长为 :根号(x2-x1)^2+(y2-y1)^2
另两边中点为((x1+x3)/2,(y1+y3)/2),和((x2+x3)/2,(y2+y3)/2)
这两中点距离为:根号((x2+x3)/2-(x1+x3)/2)^2+((y2+y3)/2-(y1+y3)/2)^2
最后化简时将x3,y3消掉正好中位线长为其对应边长的一半
定理的逆定理
逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC,DE=BC/2,则D是AB的中点,E是AC的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//BC,则E是AC的中点,DE=BC/2
【证法①】
取AC中点G ,联结DG
则DG是三角形ABC的中位线
∴DG∥BC
又∵DE∥BC
∴DG和DE重合(过直线外一点,有且只有一条直线与已知直线平行)
图形
 ##
##

-
新款凯迪拉克XT4申报图曝光 将使用碳纤维桶形座椅
2025-09-22 16:44:18 查看详情 -
新款凯迪拉克CT6申报图 将使用碳纤维桶形座椅
2025-09-22 16:44:18 查看详情 -
NL型尼龙内齿圈鼓形齿式联轴器
2025-09-22 16:44:18 查看详情


 求购
求购






