- 对称双线性型

对称双线性型
基本介绍
定义
定义1设![]() 是
是![]() 上的双线性型,若对
上的双线性型,若对![]() 中任意向量
中任意向量![]() 有
有
![]() 则称
则称![]() 是
是![]() 上的对称双线性型。
上的对称双线性型。
明显地,![]() 是对称双线性型的充要条件是,
是对称双线性型的充要条件是,![]() 的矩阵是对称的。
的矩阵是对称的。
定义2设![]() 是V上的双线性型,若对V中任意向量
是V上的双线性型,若对V中任意向量![]() 有
有
![]() 则称
则称![]() 是V上的反对称双线性型。
是V上的反对称双线性型。
同样有,![]() 是反对称双线性型的充要条件是,
是反对称双线性型的充要条件是,![]() 的矩阵是反对称的。显然,V上的一个任意的双线性型都可以表示成对称的和反对称的双线性型的和,而且,这种表示法是惟一的[2]。
的矩阵是反对称的。显然,V上的一个任意的双线性型都可以表示成对称的和反对称的双线性型的和,而且,这种表示法是惟一的[2]。
相关定理
同一个双线性型![]() 对不同的基的矩阵是不同的,并且矩阵间具有合同关系,现在我们讨论,在V中能否找到一组适当的基,使双线性型
对不同的基的矩阵是不同的,并且矩阵间具有合同关系,现在我们讨论,在V中能否找到一组适当的基,使双线性型![]() 对这基的矩阵具有较简便的形式,或者说,一个矩阵是否与对角形矩阵合同。(文中关于定理的证明请参考相应书籍)。
对这基的矩阵具有较简便的形式,或者说,一个矩阵是否与对角形矩阵合同。(文中关于定理的证明请参考相应书籍)。
定理1设![]() 是数域K上n维线性空间V的对称双线性型,则V中存在一组基,使
是数域K上n维线性空间V的对称双线性型,则V中存在一组基,使![]() 对这基的矩阵是对角矩阵[2]。
对这基的矩阵是对角矩阵[2]。
显然,定理1有下述两种不同的提法:
(1)对称矩阵必与对角形矩阵合同;
(2)对称双线性型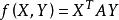 ,用适当的坐标变换
,用适当的坐标变换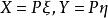 ,可化为标准形
,可化为标准形
![]() 这里
这里
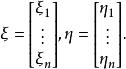
实对称双线性型
以下讨论实数域上线性空间V的对称双线性型(简称实对称双线性型)。
定理2设![]() 是实对称双线性型,
是实对称双线性型,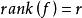 ,则V中存在一组基,使
,则V中存在一组基,使![]() 对这基的矩阵是
对这基的矩阵是
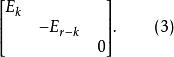 对应定理1之(2),这里的标准形是
对应定理1之(2),这里的标准形是
![]() 我们把这种形式的标准形称为
我们把这种形式的标准形称为![]() 的规范形。
的规范形。
定理3设![]() 是实对称双线性型,
是实对称双线性型,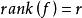 ,则在
,则在![]() 的对角形矩阵(3)中,“+1”的个数k是惟一的,因而“-1”的个数
的对角形矩阵(3)中,“+1”的个数k是惟一的,因而“-1”的个数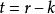 也是惟一的,即
也是惟一的,即![]() 的规范形是惟一的。
的规范形是惟一的。
在![]() 的规范形中,我们把正项个数k叫
的规范形中,我们把正项个数k叫![]() 的正惯性指数,负项个数
的正惯性指数,负项个数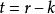 叫
叫![]() 的负惯性指数,正惯性指数与负惯性指数的差叫
的负惯性指数,正惯性指数与负惯性指数的差叫![]() 的符号差。
的符号差。
人所共知,实对称矩阵可用正交矩阵化为实对角形矩阵,因此对于n维实内积空间中的对称双线性型,又可得
定理4设![]() 是n维实内实积空间V的对称双线性型,
是n维实内实积空间V的对称双线性型,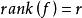 ,则V中必存在一组标准正交基,使
,则V中必存在一组标准正交基,使![]() 对这组基的矩阵是
对这组基的矩阵是
![]() 其中
其中 是
是![]() 的矩阵的不等于零的特征根,而且它的对角阵是惟一的。此定理也常常被说成为实内积空间的对称双线性型可用正交变换化为标准形[2]。
的矩阵的不等于零的特征根,而且它的对角阵是惟一的。此定理也常常被说成为实内积空间的对称双线性型可用正交变换化为标准形[2]。
复对称双线性型
最后讨论复数域上线性空间V的对称双线性型(简称复对称双线性型),并且只讨论特殊的复对称双线性型,即埃尔米特型。
定义设V是复数域C上的有限维线性空间,若对任意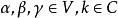 ,映射
,映射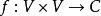 具有性质:
具有性质:
(1)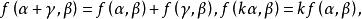 即
即![]() 对于第一个变量是线性的;
对于第一个变量是线性的;
(2)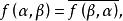 则称
则称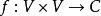 是V上的一个埃尔米特型。
是V上的一个埃尔米特型。
由(1)与(2),可推出:
![]()
![]() 即
即![]() 对于第二个变量是共轭线性的。
对于第二个变量是共轭线性的。
埃尔米特型与实对称双线性型具有相对应的性质,而且证明方法也类似,所以在下面只把结果列出。
设![]() 是V上的一个埃尔米特型,它对基
是V上的一个埃尔米特型,它对基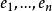 的短阵是A,
的短阵是A,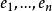 到
到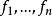 的过渡矩阵是P,则
的过渡矩阵是P,则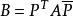 或
或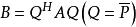 是
是![]() 对
对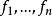 的矩阵。
的矩阵。
设A,B均为n阶矩阵,若存在可逆矩阵Q,使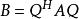 ,则称A与B是埃尔米特合同的;由此可以说,同一个埃尔米特型对不同基的矩阵是埃尔米特合同的。矩阵间的埃尔米特合同具有自反性,对称性和传递性,而且埃尔米特型
,则称A与B是埃尔米特合同的;由此可以说,同一个埃尔米特型对不同基的矩阵是埃尔米特合同的。矩阵间的埃尔米特合同具有自反性,对称性和传递性,而且埃尔米特型![]() 的矩阵的秩与基的选择无关。
的矩阵的秩与基的选择无关。
设![]() 是埃尔米特型,
是埃尔米特型,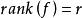 ,则有
,则有
(1)V中必存在一组基,使![]() 对这组基的矩阵是对角矩阵
对这组基的矩阵是对角矩阵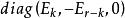 ,其中“+1”的个数是是惟一的,因而“一1”的个数
,其中“+1”的个数是是惟一的,因而“一1”的个数![]() 也是惟一的;
也是惟一的;
(2)V中必存在一组标准正交基,使![]() 对这组基的矩阵是对角矩阵
对这组基的矩阵是对角矩阵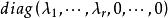 ,其中
,其中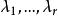 是
是![]() 的矩阵的不等于零的特征根,而且这对角阵是惟一的[2]。
的矩阵的不等于零的特征根,而且这对角阵是惟一的[2]。

-
江铃宝典堪称商用皮卡常青树 江铃新宝典VS长城风骏7(图文)
2025-06-17 06:29:13 查看详情 -
新款斯巴鲁BRZ上市 雪佛兰开拓者将推5款车型
2025-06-17 06:29:13 查看详情 -
全新紧凑型SUV/上半年上市 别克昂科拉PLUS最新谍照
2025-06-17 06:29:13 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-06-17 06:29:13 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-06-17 06:29:13 查看详情 -
将于1月6日上市 450六座版车型上市
2025-06-17 06:29:13 查看详情 -
捷途X95热爱Pro版上市 别克微蓝6插混车型上市
2025-06-17 06:29:13 查看详情 -
欧拉闪电猫将于10月31日上市 新增1.5T车型
2025-06-17 06:29:13 查看详情 -
25T车型上市 预售价17.77
2025-06-17 06:29:13 查看详情 -
凯迪拉克CT6新车型上市 W帅气亮相
2025-06-17 06:29:13 查看详情


 求购
求购

