概率图模型

概率图模型是一类用图形模式表达基于概率相关关系的模型的总称。概率图模型结合概率论与图论的知识,利用图来表示与模型有关的变量的联合概率分布。近10年它已成为不确定性推理的研究热点,在人工智能、机器学习和计算机视觉等领域有广阔的应用前景。

概率图理论共分为三个部分，分别为概率图模型表示理论，概率图模型推理理论和概率图模型学习理论。

基本的概率图模型包括 贝叶斯网络、 马尔可夫网络和隐马尔可夫网络。

基本的Graphical Model 可以大致分为两个类别：贝叶斯网络(Bayesian Network)和马尔可夫随机场(Markov Random Field)。它们的主要区别在于采用不同类型的图来表达变量之间的关系：贝叶斯网络采用有向无环图(Directed Acyclic Graph)来表达因果关系，马尔可夫随机场则采用无向图(Undirected Graph)来表达变量间的相互作用。这种结构上的区别导致了它们在建模和推断方面的一系列微妙的差异。一般来说，贝叶斯网络中每一个节点都对应于一个先验概率分布或者条件概率分布，因此整体的联合分布可以直接分解为所有单个节点所对应的分布的乘积。而对于马尔可夫场，由于变量之间没有明确的因果关系，它的联合概率分布通常会表达为一系列势函数（potential function）的乘积。通常情况下，这些乘积的积分并不等于1，因此，还要对其进行归一化才能形成一个有效的概率分布——这一点往往在实际应用中给参数估计造成非常大的困难。

概率图模型有很多好的性质

提供了一种简单的可视化概率模型的方法，有利于设计和开发新模型；

通过对图的深入研究了解概率模型的性质；

用于表示复杂的推理和学习运算，简化了数学表达；

概率图模型的表示方法,研究如何利用概率网络中的独立性来简化联合概率分布的方法表示。概率图模型能有效处理不确定性推理，从样本数据中准确高效地学习概率图模型是其在实际应用中的关键问题.概率图模型的表示由参数和结构两部分组成，PGM的分类如图1．：

（1）根据边有无方向性分类；

（2）根据表示的抽象级别不同分类。

根据边有无方向性，PGM可以分为三类

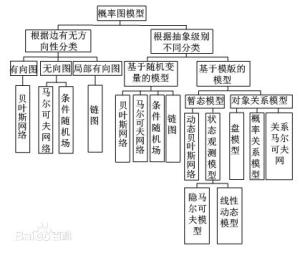（1）有向图模型，也称为贝叶斯网（BayesianNetwork，BN），其网络结构使用有向无环图；

（2）无向图模型,也称为马尔可夫网（MarkovNetwork，MN），其网络结构为无向图；

（3） 局部有向模型，即同时存在有向边和无向边的模型，包括条件随机场（ConditionalRandomField，CRF）和链图（ChainGraph）．

　　根据表示的抽象级别不同，PGM可分两类：

（1）基于随机变量的概率图模型，如贝叶斯网、马尔可夫网、条件随机场和链图等；

（2）基于模板的概率图模型．这类模型根据应用场景不同又可分为两种：

（a）为暂态模型，包括动态贝叶斯网（Dynamic Bayesian Network，DBN）[6]和状态观测模型，其中状态观测模型又包括线性动态系统（Linear Dynamic System，LDS）和隐马尔可夫模型（Hidden Markov Model，HMM）；

（b）为对象关系领域的概率图模型，包括盘模型（Plate Model，PM）、概率关系模型（Probabilistic Relational Model，PRM）和关系马尔可夫网（Relational Markov Network，RMN）.

　　总结如下

（1）单个节点上的条件概率分布的表示模型及其引起的独立性,包括表格CPD、确定性CPD、特定上下文CPD、因果影响CPD、高斯模型和混合模型,并把单个分布模型推广到指数分布族中。

（2）贝叶斯网络中的独立性以及图与概率分布的关系,高斯分布和指数分布族的贝叶斯网络表示理论。马尔可夫网络的参数化问题及其独立性,高斯分布和指数分布族的马尔可夫网络表示理论。

（3）两种局部有向图模型:条件随机场和链图。

（4）基于模板的概率模型表示,包括动态贝叶斯网络和状态观测模型这两种暂态模型,

（5）盘模型和概率关系模型这两种对象关系领域的有向概率模型,对象关系领域的无向表示。

概率图模型学习算法分为参数学习与结构学习. 基于概率图模型学习分为概率网络的参数学习与结构学习算法，并根据数据集是否完备而分为确定性不完备，随机性不完备各种情况下的参数学习算法，针对结构学习算法特点的不同，结构学习算法归纳为基于约束的学习、基于评分搜索的学习、混合学习、动态规划结构学习、模型平均结构学习和不完备数据集的结构学习.

根据网络结构与查询问题类型的不同,概率图模型的推理算法有

（1）贝叶斯网络与马尔可夫网络中解决概率查询问题的精确推理算法与近似推理算法,其中具体包括精确推理中的VE算法、递归约束算法和团树算法,以及近似推理中的变分近似推理和抽样近似推理算法;

　　（2）解决MAP查询问题的常用推理算法;

　　（3）混合网络的连续与混合情况阐述其推理算法;

　　（4）暂态网络的精确推理、近似推理以及混合情况下的推理。