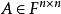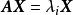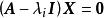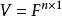- 特征子空间

特征子空间
定义
方阵的属于特征值的特征向量是齐次线性方程组即的非零解。此方程组的解集是的子空间,称为的属于特征值的特征子空间。
线性空间上线性变换的属于特征值:的全体特征向量与零向量构成的集合。
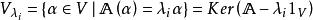 是
是![]() 的子空间,称为
的子空间,称为![]() 的属于特征值
的属于特征值![]() 的特征子空间。
的特征子空间。
只要求出了特征子空间的![]() 的一组基,基向量的全体非零线性组合就是全体特征向量。
的一组基,基向量的全体非零线性组合就是全体特征向量。
同一线性变换![]() (或方阵
(或方阵![]() )的属于不同特征值
)的属于不同特征值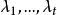 的特征子空间
的特征子空间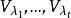 之和是直和,属于不同特征值的特征向量
之和是直和,属于不同特征值的特征向量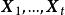 线性无关。[2]
线性无关。[2]
对角化条件
![]() 上线性变换
上线性变换![]() 如果在某组基下的矩阵
如果在某组基下的矩阵![]() 是对角阵,就称
是对角阵,就称![]() 可对角化。
可对角化。
![]() 在基M下的矩阵是对角阵
在基M下的矩阵是对角阵![]() M的向量全部是
M的向量全部是![]() 的特征向量
的特征向量![]() 各特征子空间的直和等于
各特征子空间的直和等于![]() 。
。
方阵![]() 如果相似于对角阵,就称
如果相似于对角阵,就称![]() 可对角化。
可对角化。
![]()
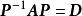 是对角阵
是对角阵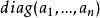
![]() P的各列是的特征向量:
P的各列是的特征向量: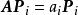 。
。
![]() 可对角化
可对角化![]()
![]() 在任何一组基下的矩阵可对角化。[2]
在任何一组基下的矩阵可对角化。[2]
几何重数与代数重数
设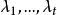 是方阵A的全部不同的特征值,每个特征值
是方阵A的全部不同的特征值,每个特征值![]() 在特征多项式
在特征多项式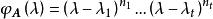 中的重数
中的重数![]() 称为
称为![]() 的代数重数,特征子空间
的代数重数,特征子空间![]() 的维数
的维数![]() 称为
称为![]() 几何重数,每个特征值
几何重数,每个特征值![]() 的几何重数≥1且≤代数重数。
的几何重数≥1且≤代数重数。
![]() 可对角化
可对角化![]() 所有的特征值的几何重数等于代数重数。
所有的特征值的几何重数等于代数重数。
特殊情形:如果n阶方阵![]() 有n个不同的特征值,则每个特征值的代数重数和几何重数都等于1,
有n个不同的特征值,则每个特征值的代数重数和几何重数都等于1,![]() 可对角化。[2]
可对角化。[2]
例题分析与解答
设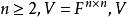 的线性变换
的线性变换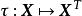 将
将![]() 中每个方阵
中每个方阵![]() 送到它的转置
送到它的转置![]() 。求
。求![]() 的特征值和特征向量,
的特征值和特征向量,![]() 是否可对角化?
是否可对角化?
解对任意![]() 有
有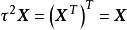 ,可见
,可见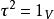 是
是![]() 上的恒等变换,
上的恒等变换,![]() 的属于每个特征值
的属于每个特征值![]() 的特征向量
的特征向量![]() 满足
满足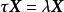 从而
从而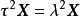 ,将
,将![]() 代入得
代入得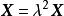 ,从而
,从而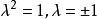 。
。
![]() 是
是![]() 的属于特征值1的特征向量
的属于特征值1的特征向量![]()
![]() 且
且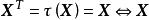 是非零对称方阵。
是非零对称方阵。
![]() 是
是![]() 的属于特征值-1的特征向量
的属于特征值-1的特征向量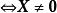 且
且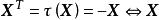 是非零斜对称方阵。
是非零斜对称方阵。
![]() 存在一组由特征向量组成的基:
存在一组由特征向量组成的基:
![]()
![]() 在这组基下的矩阵是对角阵
在这组基下的矩阵是对角阵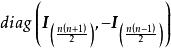 。[2]
。[2]

相关百科
-
实拍江铃新宝典(图文) 空间满足家用
2025-09-21 12:03:49 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-09-21 12:03:49 查看详情 -
江铃福特轻客持续打造最优TCO 空间满足家用
2025-09-21 12:03:49 查看详情 -
航天恒星空间技术应用有限公司
2025-09-21 12:03:49 查看详情 -
上海车展实拍江铃福特领裕 空间满足家用
2025-09-21 12:03:49 查看详情


 求购
求购