- 两平面平行

两平面平行
两平面平行的定义
两平面平行是两平面间的一种位置关系,如果两个平面没有公共点,我们说这两个平面互相平行,一个平面称为另一个平面的平行平面。
两平面平行的性质定理
定理1两平面平行,其中一个平面内的直线必平行于另一个平面。
定理2如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
定理3一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面[1]。
例如图1,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1C,B1C1,C1D1的中点,求证:
(1)AP⊥MN;
(2)平面MNP∥平面A1BD。
 图1
图1
证明(1)连结BC1,B1C,则B1C⊥BC1,BC1是AP在面BB1C1C上的射影,
∴ AP⊥B1C.
又B1C∥MN,
∴ AP⊥MN.
(2)连结B1D1.
∵ P,N分别是D1C1,B1C1的中点,
∴ PN∥B1D1.又B1D1∥BD,
∴ PN∥BD.
又PN不在平面A1BD上,
∴ PN∥平面A1BD.
同理,MN∥平面A1BD.
又PN∩MN=N,
∴ 平面PMN∥平面A1BD。
说明将空间问题转化为平面问题,是解决立体几何问题的重要策略.解决这类问题关键在于选择或添加适当的平面或线。由于M,N,P都为中点,故添加B1C,BC1作为联系的桥梁[1]。
两平面平行的判定
设两平面![]() 的方程分别为
的方程分别为
![]()
![]() 其法线向量分别为
其法线向量分别为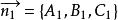 和
和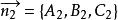 。
。
两平面平行的充要条件:
![]() 即
即
![]() 用分量来表示为:
用分量来表示为:
![]() 亦即
亦即
![]() 或
或
![]()
若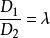 ,即
,即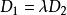 ,则平面
,则平面![]() 的方程为:
的方程为:
![]() 即:
即:
![]() 与平面β的方程一致,所以两平面重合,由此我们看出:
与平面β的方程一致,所以两平面重合,由此我们看出:
两平面![]() 平行的充要条件是
平行的充要条件是
![]()
两平面![]() 重合的充要条件是
重合的充要条件是
![]()
两平面相交
即![]() 不平行,即
不平行,即
![]() 这时两平面相交时所得直线的方程可用方程组
这时两平面相交时所得直线的方程可用方程组
![]() 来表示[2]。
来表示[2]。
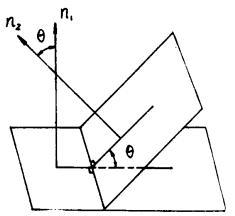 图2
图2
为了确定起见,规定两平面组成的二面角中,不大于直角的为两平面的交角,记作θ,如图2,![]() 所成的夹角θ就是两法线向量
所成的夹角θ就是两法线向量![]() 的夹角θ,即
的夹角θ,即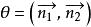 (图1),且[2]
(图1),且[2]
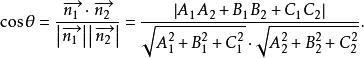 特别地,当
特别地,当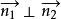 时,
时,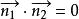 , 故又可以得两平面互相垂直的充要条件为
, 故又可以得两平面互相垂直的充要条件为
![]()

-
平面二次包络环面蜗杆传动
2025-11-03 04:51:12 查看详情 -
奔驰S 平行进口实拍
2025-11-03 04:51:12 查看详情 -
天津地区奔驰GLS450 平行进口实拍
2025-11-03 04:51:12 查看详情


 求购
求购







