线性化

严格的讲，实际物理原件和系统都是非线性的。

叠加原理不适应于非线性系统，这给求解非线性系统带来了不便，因此需要对所研究的系统做线性化处理。

非线性系统进行线性化的条件：

非线性函数是连续函数；系统在预定工作点附近小偏差运行，即变量的变化范围很小。

如图1所示为连续变化的非线性函数为：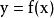

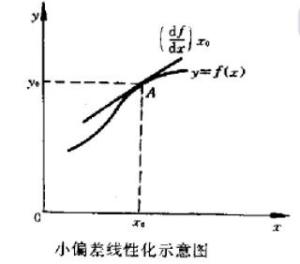图1线性化方法：

把非线性函数在工作点附近展开成泰勒级数，略去高次项，使得一个以增量为变量的线性函数：

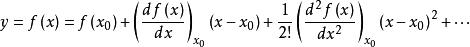当增量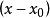很小时，略去其高次幂项，则

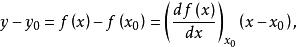
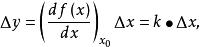
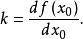
k是比例系数，它是函数在工作点A点的切线斜率。

将线性增量方程代入系统微分方程，便可得系统线性化方程。

在函数的一个点处的线性化函数是：

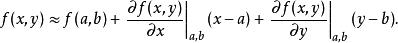
多变量函数的一般方程在一个点处的线性化方程是：

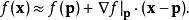
其中是变量的向量，是线性化的工作点^[1]。

1）线性化是相随某已工作点，工作点不同，线性化方程的系数也不同；

2）偏差越小，线性化精度越高；

3）线性化适用于连续变化的单值函数；

4）式中变量是增量，不是绝对值，公式称为增量方程式；

5）额定工作点若是坐标原点，增量可以写成绝对量；

6）当增量并不是很小时，在进行线性化时，为了验证容许的误差值，需要分析泰勒式中的余项。

在自治系统的稳定性分析中，可以使用在双曲平衡点评估的雅可比矩阵的特征值来确定该平衡的性质。这是线性化定理的内容。

在微观经济学中，决策规则可以在线性化的状态空间方法下近似。

在数学优化中，成本函数和内部的非线性分量可以线性化，以便应用诸如Simplex算法的线性求解方法。优化的结果可以更有效地得到全局最优的解^[2]。

在多物理场系统中，涉及多个彼此相互作用的物理场的系统，可以执行关于每个物理场的线性化。该系统关于每个场的线性化会形成线性化的单片方程系统，其可以使用单片迭代解决方案如牛顿 - 拉夫逊（Newton-Raphson）方法来求解。这样的例子包括机械和声场系统的MRI扫描仪系统等^[3]。