- 球极坐标系

球极坐标系
定义
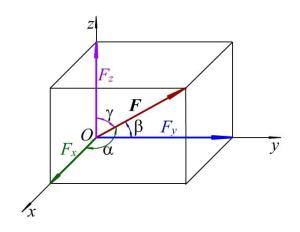
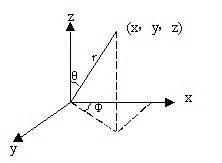 设空间任意点
设空间任意点![]() ,它在直角坐标系中的坐标为
,它在直角坐标系中的坐标为![]() ,则 如下的有序数组
,则 如下的有序数组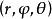 称为点
称为点![]() 的球坐标:坐标
的球坐标:坐标![]() 是点
是点![]() 到原点的距离,
到原点的距离,![]() 是通过
是通过![]() 轴和点
轴和点![]() 的半平面与坐标面
的半平面与坐标面![]() 所构成的角;
所构成的角;![]() 是线段
是线段![]() 与
与![]() 轴正方向的夹角,因此,在空间中这些坐标的变化范围是:
轴正方向的夹角,因此,在空间中这些坐标的变化范围是:
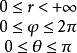
在球坐标系中,坐标曲面分别是:
![]() :以原点为重心,
:以原点为重心,![]() 为半径的球面;
为半径的球面;
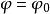 :以
:以![]() 轴为边并与坐标平面
轴为边并与坐标平面![]() 构成角
构成角![]() 的半平面。
的半平面。
![]() :以原点为顶点,
:以原点为顶点,![]() 轴为轴,半顶角为
轴为轴,半顶角为![]() 的圆锥面。[1]
的圆锥面。[1]
直角坐标和球坐标的对应关系
直角坐标和球坐标的对应关系如下:
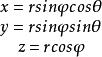
于是在球坐标中,球面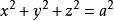 的方程为
的方程为![]() ,球面
,球面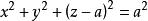 的方程为
的方程为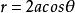 ,柱面
,柱面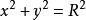 的方程为
的方程为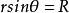 。[1]
。[1]

相关百科
-
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-09-22 04:28:09 查看详情 -
广汽本田全新皓影正式上市 宝马1系M运动曜熠版上市
2025-09-22 04:28:09 查看详情 -
雪佛兰开拓者正式上市 全新宝马7系/i7正式上市
2025-09-22 04:28:09 查看详情 -
珠海英菲尼迪Q50L优惠达5.4万 成都新宝马3系优惠5万元
2025-09-22 04:28:09 查看详情 -
成都新宝马3系优惠5万元 再送装潢礼包
2025-09-22 04:28:09 查看详情 -
i/汉EV创世版有望3月16日上市 中期改款5系再曝光
2025-09-22 04:28:09 查看详情 -
前脸更像7系/或将于中上市 旗下首款纯电动车型
2025-09-22 04:28:09 查看详情 -
吉利缤越PRO家族正式上市 大众ID.7第二季度全球首发
2025-09-22 04:28:09 查看详情 -
成都丰田锐志最高优惠2.7万元 青岛宝马8系现金优惠达9万元
2025-09-22 04:28:09 查看详情 -
斯威G01改款车型将于10月上市 前脸更像7系/或将于中上市
2025-09-22 04:28:09 查看详情


 求购
求购

