- 薄板理论
薄板理论
薄板理论的内容
根据有关变形假设,建立板弯曲后中面的挠度微分方程,并利用边界条件求解,得出板中面的弯曲面,进而算出板的内力分量,如弯矩、扭矩、剪力,等等。
微分方程
薄板理论是一个近似理论。薄板挠度微分方程是以下面三个假设为基础的:①原垂直于板中面的线段仍垂直于变形后的中面;垂直于中面的正应力(见应力)远小于平行于中面的应力分量,故可以忽略;③在垂直于板中面的载荷作用下发生弯曲时,板中面不受拉伸。其中①和③称为基尔霍夫假设。根据这些假设导出的微分方程适用于小挠度情况,即挠度和板厚度相比为一小量。
在垂直于板中面的分布载荷作用下(图1),薄板挠度的微分方程为:
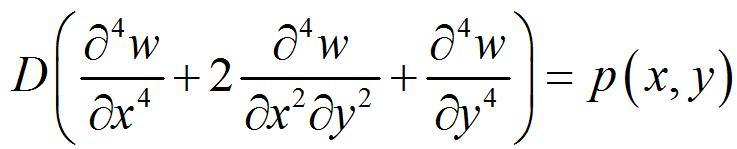
式中p(x,y)为垂直于板面的分布载荷;w为载荷作用下板中面各点沿z方向的位移(即挠度);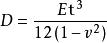
为板的弯曲刚度,E为板材料的弹性模量,v为泊松比(见材料的力学性能);t为板厚。
如果在板的中面内还有张力Nx、Ny和剪力Nxy(图2),则微分方程为: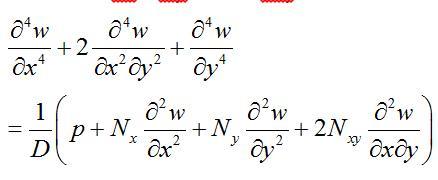
如果薄板被弹性地基支承,根据温克勒假设,即地基的反作用力和沉陷深度成正比,则有:
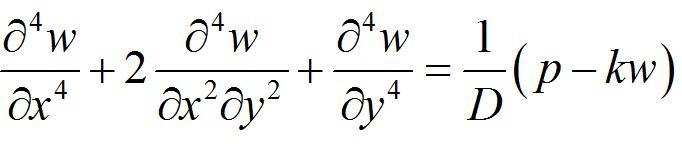
式中k为地基的弹性模量。
对于正交各向异性板,弯曲面的微分方程为:
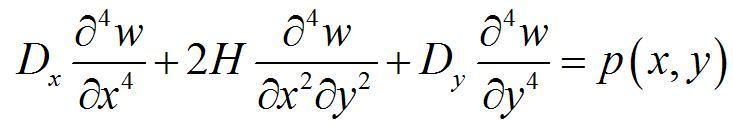
式中的Dx、H、Dy均为正交各向异性板的有关常数。
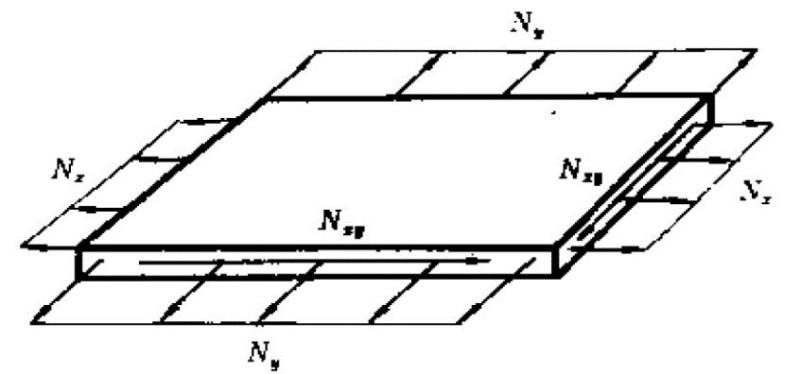 图2 板中的内力
图2 板中的内力
上述方程通过坐标变换还可写成其他形式,以便求解其他形状的板。例如通过极坐标变换,可得到求解各向同性圆板弯曲面的微分方程如下:
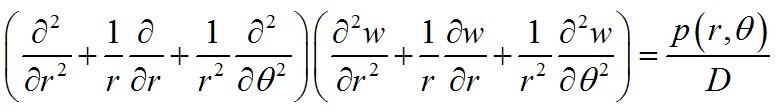
边界条件
对不同的边界情况,边界条件有所不同:
①固定边沿边缘各点的挠度和斜度均为零。在直角坐标系中,若x=a为固定边,则
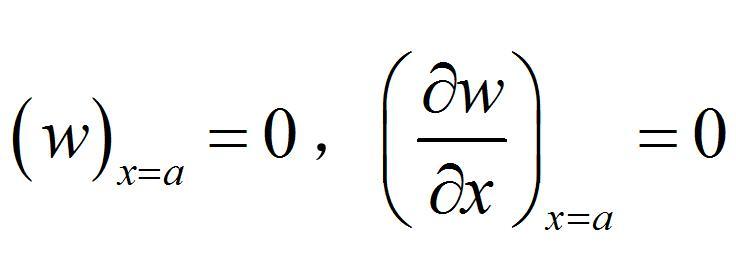
②简支边(注:此处空格)沿简支边各点的挠度和弯矩M均为零。若x=a为简支边,则
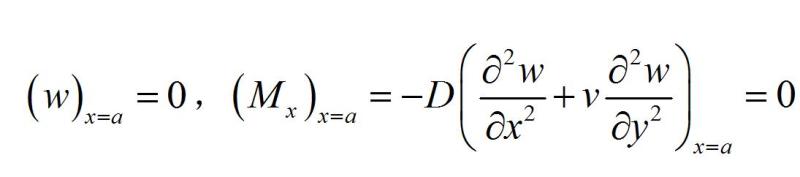
③自由边(注:此处空格)沿自由边各点的弯矩和剪力V为零。若x=a为自由边,则
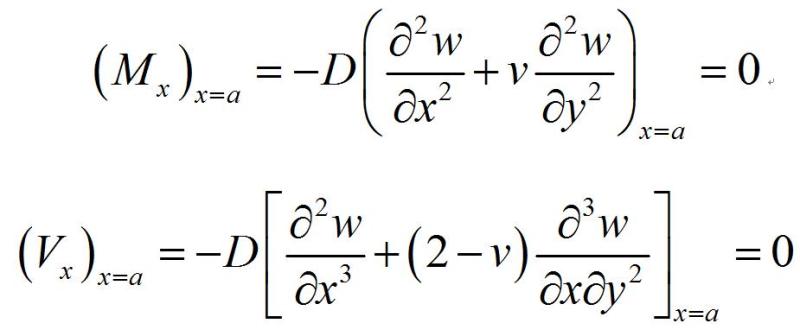
④自由角点(注:此处空格)若x=a,y=b是一个自由角点,则角点的反力R为零,即
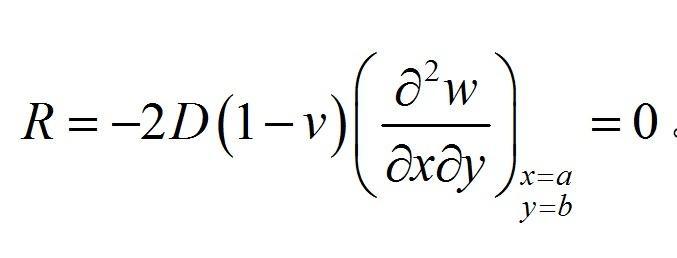
求解
有两种途径,一是求出既满足微分方程又满足边界条件的精确解(如莱维法,纳维法);二是当得不到精确解时,采用各种近似方法求解,例如有限元法、有限差分方法等数值方法和能量方法。出于工程实际的需要,人们对矩形板和圆板的研究较多。



 求购
求购










